Exponential Signal Reconstruction with Deep Hankel Matrix Factorization(中文，English)
黄奕晖†,1, 赵金奎†,1, 王孜1, 郭迪2, 屈小波*,1
1 厦门大学，电子科学系，生物医学智能云研发中心, 健康医疗大数据国家研究院，中国，厦门;
2 厦门理工学院，计算机与信息工程学院，中国，厦门;
概要:
指数信号是信号处理领域中最重要的基本信号类型之一，在通信、成像、电子系统及核磁共振等应用中都有用到。由于加速采样或其它不可避免的原因，实际采样得到的信号有时不能满足奈奎斯特准则，导致采集数据丢失从而造成信号失真. 如何对欠采样指数信号进行重建是学术界与工业界密切关注的前沿问题。传统最优化算法计算最优解所需大量迭代次数较为耗时。而对于最前沿的深度学习方法，信号尤其是低强度弱峰的重建误差仍需要降低。
本文通过模仿现有的基于模型的低秩汉克尔重建方法，提出了一种基于深度汉克尔矩阵分解的神经网络DHMF。网络约束了指数信号转汉克尔矩阵后的低秩特性，其设计参靠了基于矩阵分解的无需奇异值分解的低秩汉克尔矩阵补全方法。由于一直可以完全通过仿真信号训练网络，我们通过仿真指数信号来学习由欠采样信号至全采样信号间的映射。
实验表明，相较于最前沿的基于模型的方法与深度学习方法，所提DHMF比前者更快，比后者更具可解释性。同时，DHMF在仿真数据与真实磁共振波谱上都有着更低的重建误差，并能更好地保护弱峰。
方法:
本文所提DHMF包含 P, Q, D三个更新模块以及一个数据校验模块(Fig. 1).
Fig. 1. DHMF网络结构. (a) 第 k 个迭代块结构, (b)基本DHMF所采用的时域卷积P/Q模块, (c) 加强型DHMF所采用的频域卷积P/Q模块, (d) 密集连接卷积神经网络。
第
个迭代块中各模块的设计为:
其中
和
表示更新算子,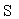 
表示数据校验算子, 
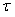表示步长,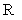 
表示将信号向量转为汉克尔矩阵的算子，
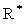为其逆算子。
最终的损失函数为：
,
其中
是正则化参数. 下标 q表示所有Q 个采样序列中第q个训练数据。
是网络中可学习参数的集合，包括P，Q更新模块中的卷积层及批归一化层中的可学习权重。
结果:
我们在仿真指数信号及实测的磁共振波谱上将所提DHMF与三种最前沿的方法进行对比。对比方法包括LRHM [8], LRHMF [10]和DLNMR [14]. LRHM与LRHMF是典型的迭代优化方法， DLNMR 是指数函数重建任务中最前沿的深度学习方法。
1. 网络的可解释性
Fig.2 表明DHMF隐性学习了具有低秩特性的近似解，相较DLNMR在网络重建中有着更好的解释性。
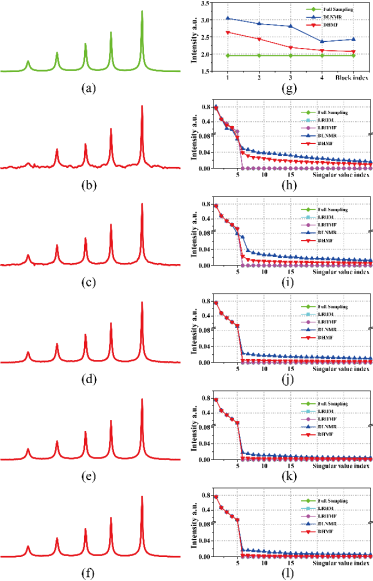
Fig. 2.各迭代块的重建波谱与奇异值分析 (a)全采样波谱, (b)-(f)第1至第5个迭代块的重建波谱 (g) 时域信号汉克尔矩阵的核范数, (h)-(l)各迭代块输出的对应奇异值。
2. 仿真信号重建
Fig.3 表明，相较其他方法，DHMF能够重建含更多谱峰的指数信号或使用更少的采样点数进行重建。Fig.4 表明DHMF能够重建出与全采样波谱最一致的峰形与谱峰强度，并在弱峰重建中有着最高的相关系数。
Fig. 3. 仿真数据在四种方法上的平均重建误差。（a） LRHM（b） LRHMF（c）DLNMR（ d） DHMF。注：每种颜色对应了在 100 次蒙特卡洛实验中方法的平均 RLNE。红线（或白线）表示了重建误差 RLNE 为 0.1（或 0.2）时的边界，在边界上方（或下方）的区域内，方法的重建误差会高于（或低于）该边界。其中 DLNMR 未能有重建误差小于 0.1 的区域，因此其红色边界没有下方区域。
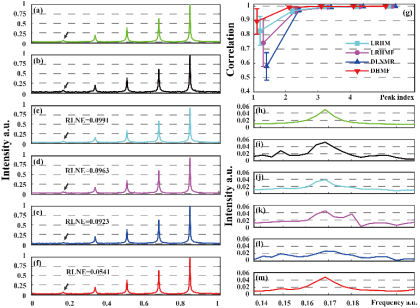
Fig. 4. 四种对比方法在25%采样率的低谱峰仿真数据的重建效果。（a）是全采样的无噪信号，（b）是额外添加了标准差为 0.05 的高斯噪声的有噪信号，（c）到（f）分别是LRHM,LRHMF,DLNMR 和 DHMF 的重建信号，（h）到（m）表示将箭头所指的弱峰局部放大。（g）是各个谱峰的皮尔森线性相关系数。
3. 实测NMR信号重建
在1H-15N TROSY 波谱(Fig. 5(a)) 与 1H-15N HSQC 波谱(Fig. 6(a))的重建表明，DHMF 在实测NMR波谱上有着最可信的重建结果。
Fig. 5. 25%采样率的泛素 2D 1H-15N TROSY谱的重建效果。（a）是全采样的 NMR 谱，（b）到（e）分别是 LRHM， LRHMF， DLNMR 和 DHMF的重建谱图。这里我们额外在全采样信号中加入了标准差为 0.02 的高斯噪声。（f）和（g）箭头所指的，在一维 15N 序列上的谱峰局部放大。绿色，青色，紫色，蓝色和红色分别表示全采样谱， LRHM， LRHMF， DLNMR 和 DHMF 的重建谱。
Fig. 6. 细胞溶质 CD79b 蛋白质的2D 1H-15N HSQC谱的重建效果。（a）是全采样的 NMR 谱，（b）到（e）分别是 LRHM， LRHMF， DLNMR 和 DHMF的重建谱图。这里我们额外在全采样信号中加入了标准差为 0.01 的高斯噪声。（f）和（g）箭头所指的，在一维 15N 序列上的谱峰局部放大。绿色，青色，紫色，蓝色和红色分别表示全采样谱， LRHM， LRHMF， DLNMR 和 DHMF的重建谱。
下载:
数据集：
点击该链接下载训练集，仿真数据，以及欠采样实测NMR波谱。
论文:
Arxiv: https://arxiv.org/abs/2007.06246
引用:
Yihui Huang, Jinkui Zhao, Zi Wang, Di Guo, Xiaobo Qu. “Complex exponential signal recovery with deep hankel matrix factorization,” arXiv preprint, arXiv:2007.06246, 2020.
致谢:
1）数据与硬件支持
作者感谢Vladislav Orekhov 与 Maxim Mayzel提供的磁共振波谱数据、NVIDIA公司提供的GPU。以及中国移动提供的云服务。
2）基金
本工作获得了国际自然科学基金（61971361, 61871341,及61811530021），中国国家重点研究开发计划2017YFC00108703，厦门大学南强杰出人才计划的资助。
参考文献:
[1] A. Hirose and S. Yoshida, "Generalization characteristics of complexvalued feedforward neural networks in relation to signal coherence," IEEE Trans. Neural Netw. Learn. Syst., vol. 23, no. 4, pp. 541-551, 2012.
[2] C. Qian, L. Huang, M. Cao, J. Xie, and H. C. So, "PUMA: An improved realization of MODE for DOA estimation," IEEE Trans. Aerosp. Electron. Syst., vol. 53, no. 5, pp. 2128-2139, 2017.
[3] D. Nion and N. D. Sidiropoulos, "Tensor algebra and multidimensional harmonic retrieval in signal processing for mimo radar," IEEE Trans. Signal Process., vol. 58, no. 11, pp. 5693-5705, 2010.
[4] L. Schermelleh, R. Heintzmann, and H. Leonhardt, "A guide to superresolution fluorescence microscopy," J. Cell Biol., vol. 190, no. 2, pp. 165-175, 2010.
[5] J. A. Tropp, J. N. Laska, M. F. Duarte, J. K. Romberg, and R. G. Baraniuk, "Beyond Nyquist: Efficient sampling of sparse bandlimited signals," IEEE Trans. Inf. Theory, vol. 56, no. 1, pp. 520-544, 2010.
[6] M. Vetterli, P. Marziliano, and T. Blu, "Sampling signals with finite rate of innovation," IEEE Trans. Signal Process., vol. 50, no. 6, pp. 1417-1428, 2002.
[7] M. Elad, P. Milanfar, and G. Golub, H, "Shape from moments – an estimation theory perspective," IEEE Trans. Signal Process., vol. 52, no. 7, pp. 1814-1829, 2004.
[8] X. Qu, M. Mayzel, J.-F. Cai, Z. Chen, and V. Orekhov, "Accelerated NMR spectroscopy with low-rank reconstruction," Angew. Chem.-Int. Edit., vol.54, no. 3, pp. 852-854, 2015.
[9] H. M. Nguyen, X. Peng, M. N. Do, and Z.-P. Liang, "Denoising MR spectroscopic imaging data with low-rank approximations," IEEE Trans. Biomed. Eng., vol. 60, no. 1, pp. 78-89, 2013.
[10] D. Guo, H. Lu, and X. Qu, "A fast low rank Hankel matrix factorization reconstruction method for non-uniformly sampled magnetic resonance spectroscopy," IEEE Access, vol. 5, pp. 16033-16039, 2017.
[11] J. Ying, H. Lu, Q. Wei, J.-F. Cai, D. Guo, J. Wu, Z. Chen, and X. Qu, "Hankel matrix nuclear norm regularized tensor completion for Ndimensional exponential signals," IEEE Trans. Signal Process., vol. 65, no.14, pp. 3702-3717, 2017.
[12] H. Lu, X. Zhang, T. Qiu, J. Yang, J. Ying, D. Guo, Z. Chen, and X. Qu, "Low rank enhanced matrix recovery of hybrid time and frequency data in fast magnetic resonance spectroscopy," IEEE Trans. Biomed. Eng., vol. 65, no. 4, pp. 809-820, 2018.
[13] H. Cai, J. Cai, T. Wang, and G. Yin, "Accelerated structured alternating projections for robust spectrally sparse signal recovery," IEEE Trans. Signal Process., vol. 69, pp. 809-821, 2021.
[14] X. Qu, Y. Huang, H. Lu, T. Qiu, D. Guo, T. Agback, V. Orekhov, and Z.Chen, "Accelerated nuclear magnetic resonance spectroscopy with deep learning," Angew. Chem.-Int. Edit., vol. 59, no. 26, pp. 10297-10300, 2020.
[15] K. Usevich and P. Comon, "Hankel low-rank matrix completion: Performance of the nuclear norm relaxation," IEEE J. Sel. Top. Signal Process., vol. 10, no. 4, pp. 637-646, 2016.
[16] Y. Chen and Y. Chi, "Robust spectral compressed sensing via structured matrix completion," IEEE Trans. Inf. Theory, vol. 60, no. 10, pp. 6576-6601, 2014.
[17] J. Ying, J.-F. Cai, D. Guo, G. Tang, Z. Chen, and X. Qu, "Vandermonde factorization of Hankel matrix for complex exponential signal recovery—application in fast NMR spectroscopy," IEEE Trans. Signal Process., vol.66, no. 21, pp. 5520-5533, 2018.
[18] K. Kazimierczuk and V. Y. Orekhov, "Accelerated NMR spectroscopy by using compressed sensing," Angew. Chem.-Int. Edit., vol. 50, no. 24, pp.5556-5559, 2011.
[19] X. Qu, X. Cao, D. Guo, and Z. Chen, "Compressed sensing for sparse magnetic resonance spectroscopy," in Int. Soc. Magn. Reson. Med. 18th Sci.Meet., 2010, p. 3371.
[20] D. J. Holland, M. J. Bostock, L. F. Gladden, and D. Nietlispach, "Fast multidimensional NMR spectroscopy using compressed sensing," Angew.Chem.-Int. Edit., vol. 50, no. 29, pp. 6548-6551, 2011.
[21] S. G. Hyberts, K. Takeuchi, and G. Wagner, "Poisson-gap sampling and forward maximum entropy reconstruction for enhancing the resolution and sensitivity of protein NMR data," J. Am. Chem. Soc., vol. 132, no. 7, pp.2145-2147, 2010.
[22] X. Qu, D. Guo, X. Cao, S. Cai, and Z. Chen, "Reconstruction of self-sparse 2d NMR spectra from under sampled data in the indirect dimension,"Sensors, vol. 11, no. 9, pp. 8888-8909, 2011.
[23] Z. Tu, H. Liu, J. Zhan, and D. Guo, "A fast self-learning subspace reconstruction method for non-uniformly sampled nuclear magnetic resonance spectroscopy," Applied Sciences, vol. 10, no. 11, p. 3939, 2020.
[24] E. J. Candès, J. Romberg, and T. Tao, "Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information,"IEEE Trans. Inf. Theory, vol. 52, no. 2, pp. 489-509, 2006.
[25] V. Chandrasekaran, B. Recht, P. A. Parrilo, and A. S. Willsky, "The convex geometry of linear inverse problems," Found. Comput. Math., vol. 12, no.6, pp. 805-849, 2012.
[26] T. Qiu, Z. Wang, H. Liu, D. Guo, and X. Qu, "Review and prospect: NMR spectroscopy denoising and reconstruction with low-rank Hankel matrices and tensors," Magnetic Resonance in Chemistry, vol. 59, no. 3, pp. 324-345, 2021.
[27] J.-M. Papy, L. De Lathauwer, and S. Van Huffel, "Exponential data fitting using multilinear algebra: The decimative case," J. Chemometr., vol. 23, no. 7‐8, pp. 341-351, 2009.
[28] M. Fazel, T. K. Pong, D. Sun, and P. Tseng, "Hankel matrix rank minimization with applications to system identification and realization,"SIAM J. Matrix Anal. Appl., vol. 34, no. 3, pp. 946-977, 2013.
[29] I. Markovsky, "Recent progress on variable projection methods for structured low-rank approximation," Signal Process., vol. 96, pp. 406-419, 2014.
[30] J.-F. Cai, X. Qu, W. Xu, and G. Ye, "Robust recovery of complex exponential signals from random Gaussian projections via low rank Hankel matrix reconstruction," Appl. Comput. Harmon. Anal., vol. 41, no. 2, pp.470-490, 2016.
[31] I. Markovsky and K. Usevich, "Structured low-rank approximation with missing data," SIAM J. Matrix Anal. Appl., vol. 34, no. 2, pp. 814-830, 2013.
[32] X. Peng, C. Lu, Z. Yi, and H. Tang, "Connections between nuclear-norm and Frobenius-norm-based representations," IEEE Trans. Neural Netw.Learn. Syst., vol. 29, no. 1, pp. 218-224, 2018.
[33] J.-F. Cai, E. J. Candes, and Z. Shen, "A singular value thresholding algorithm for matrix completion," SIAM J. Optim., vol. 20, no. 4, pp. 1956-1982, 2010.
[34] K. H. Jin, D. Lee, and J. C. Ye, "A general framework for compressed sensing and parallel MRI using annihilating filter based low-rank Hankel matrix," IEEE Trans. Comput. Imaging, vol. 2, no. 4, pp. 480-495, 2016.
[35] X. Zhang, D. Guo, Y. Huang, Y. Chen, L. Wang, F. Huang, Q. Xu, and X.Qu, "Image reconstruction with low-rankness and self-consistency of kspace data in parallel MRI," Med. Image Anal., vol. 63, p. 101687, 2020.
[36] Y. LeCun, Y. Bengio, and G. Hinton, "Deep learning," Nature, vol. 521, no. 7553, pp. 436-444, 2015.
[37] R. Liu, Z. Jiang, X. Fan, and Z. Luo, "Knowledge-driven deep unrolling for robust image layer separation," IEEE Trans. Neural Netw. Learn. Syst., vol. 31, no. 5, pp. 1653-1666, 2020.
[38] D. Chen, Z. Wang, D. Guo, V. Orekhov, and X. Qu, "Review and prospect: Deep learning in nuclear magnetic resonance spectroscopy," Chem.-Eur. J., vol. 26, pp. 10391-10401, 2020.
[39] Y. Yang, J. Sun, H. Li, and Z. Xu, "ADMM-CSNet: A deep learning approach for image compressive sensing," IEEE Trans. Pattern Anal.Mach. Intell., vol. 42, pp. 521-538, 2020.
[40] T. Lu, X. Zhang, Y. Huang, D. Guo, F. Huang, Q. Xu, Y. Hu, L. Ou-Yang, J. Lin, Z. Yan, and X. Qu, "pFISTA-SENSE-ResNet for parallel MRI reconstruction," J. Magn. Reson., vol. 318, p. 106790, 2020, Art no.106790.
[41] V. Monga, Y. Li, and C. Elda, Yonina, "Algorithm unrolling: Interpretable, efficient deep learning for signal and image processing," IEEE Signal Process. Mag., vol. 38, no. 2, pp. 18-44, 2021.
[42] J. Zhang and B. Ghanem, "ISTA-Net: Interpretable optimization-inspired deep network for image compressive sensing," in Proc. CVPR, 2018, pp.1828-1837.
[43] S. Gunasekar, B. Woodworth, S. Bhojanapalli, B. Neyshabur, and N.Srebro, "Implicit regularization in matrix factorization," in Proc. NIPS, 2017, vol. 30, pp. 6151-6159.
[44] S. Arora, N. Cohen, W. Hu, and Y. Luo, "Implicit regularization in deep matrix factorization," in Proc. NIPS, 2019, vol. 32, pp. 7413-7424.
[45] G. Trigeorgis, K. Bousmalis, S. Zafeiriou, and B. W. Schuller, "A deep matrix factorization method for learning attribute representations," IEEE Trans. Pattern Anal. Mach. Intell., vol. 39, no. 3, pp. 417-429, 2017.
[46] X.-R. Feng, H.-C. Li, J. Li, Q. Du, A. Plaza, and J. Emery, William; , "Hyperspectral unmixing using sparsity-constrained deep nonnegative matrix factorization with total variation," IEEE Trans. Geosci. Remote Sensing, vol. 56, no. 10, pp. 6245-6257, 2018.
[47] P. Sprechmann, A. M. Bronstein, and G. Sapiro, "Learning efficient sparse and low rank models," IEEE Trans. Pattern Anal. Mach. Intell., vol. 37, no.9, pp. 1821-1833, 2015.
[48] O. Solomon, R. Cohen, Y. Zhang, Y. Yang, Q. He, J. Luo, R. J. G. v. Sloun, and Y. C. Eldar, "Deep unfolded robust PCA with application to clutter suppression in ultrasound," IEEE Trans. Med. Imaging, vol. 39, no. 4, pp.1051-1063, 2020.
[49] N. Srebro, "Learning with matrix factorizations," Ph.D. dissertation, MIT, 2004.
[50] S. Boyd, N. Parikh, E. Chu, B. Peleato, and J. Eckstein, "Distributed optimization and statistical learning via the alternating direction method of multipliers," Found. Trends Mach. Learn., vol. 3, no. 1, pp. 1-122, 2011.
[51] G. Huang, Z. Liu, L. Van Der Maaten, and K. Q. Weinberger, "Densely connected convolutional networks," in Proc. CVPR, 2017, pp. 4700-4708.
[52] W. Lee, M. Tonelli, and J. L. Markley, "NMRFAM-SPARKY: Enhanced software for biomolecular NMR spectroscopy," Bioinformatics, vol. 31, no.8, pp. 1325-1327, 2015.
[53] D. P. Kingma and J. Ba, "Adam: A method for stochastic optimization," arXiv Preprint arXiv:1412.6980, 2014.
[54] F. Delaglio, S. Grzesiek, G. W. Vuister, G. Zhu, J. Pfeifer, and A. Bax, "NMRPipe: A multidimensional spectral processing system based on UNIX pipes," J. Biomol. NMR, vol. 6, no. 3, pp. 277-293, 1995.
[55] J. C. Hoch and A. S. Stern, NMR Data Processing. Wiley, 1996.
[56] R. Roy and T. Kailath, "ESPRIT-estimation of signal parameters via rotational invariance techniques," IEEE Trans. Acoust., Speech, Signal Process., vol. 37, no. 7, pp. 984-995, 1989.
[57]P. Stoica and R. L. Moses, Spectral Analysis of Signals. Prentice Hall, 2005