Exponential Signal Reconstruction with Deep Hankel Matrix Factorization(中文,English)
Yihui Huang†,1, Jinkui Zhao†,1, Zi Wang1, Di Guo2, Xiaobo Qu*,1
1 Electronic Science, Biomedical Intelligent Cloud R&D Center, National Institute for Data Science in Health and Medicine, Xiamen University, Xiamen, China
2 School of Computer and Information Engineering, Xiamen University of Technology, Xiamen, China
Synopsis:
Exponential function is a fundamental signal form in signal processing. Representative application fields of exponential signals include communication, imaging, electronic system and NMR spectroscopy. For fast data acquisition or other inevitable reasons, only a small amount of samples may be acquired. How to reconstruct under sampled exponentials is one of the fundamental problems and frontiers in signal processing. Existing iterative algorithms, such as low rank, are time consuming, while the reconstruction error of the state-of-the-art deep learning method, especially for the low low-intensity signals, still needs to be reduced.
In this work, we propose a deep learning neural network called Deep Hankel Matrix Factorization network (DHMF) to recover exponentials by imitating the established model-based low-rank Hankel reconstruction algorithm. Our design starts from constraining the low rank property of the Hankel matrix which is arranged from exponential signals and adopts matrix factorization-based Low-Rank Hankel Matrix Completion which are SVD-free. Given the success of the training network using solely synthetic data, we also synthesize exponentials and then feed into the network to learn the mapping from under sampled exponentials, to fully sampled exponentials.
Compared with the state-of-the-art model-based and DL-based methods, DHMF is much faster than the former, and possess a more understandable network architecture than the latter. DHMF also achieves lower reconstruction error than the compared methods on both synthetic and realistic NMR data, and can preserve the low intensity signals much better.
Method:
The proposed DHMF consists of three updating modules P, Q, D and one data consistency module (Fig. 1).
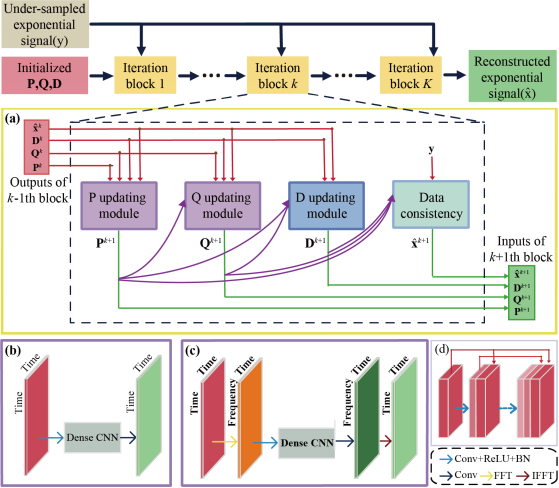
Fig. 1. The architecture of DHMF. (a) the general process of the k-th block, (b) P/Q modules with time domain convolution in the basic DHMF, (c) P/Q modules with frequency domain convolution in the enhanced DHMF, (d) dense convolutional neural network.
Each updating modules of  block are designed as:
block are designed as:
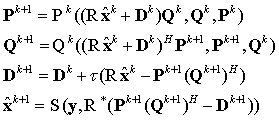
where 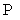 and
and 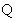 are updating operators,
are updating operators,  denotes the data consistency operator,
denotes the data consistency operator, 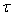 is the learning step,
is the learning step, 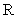 denotes the Hankel operator mapping the vector to a Hankel matrix while
denotes the Hankel operator mapping the vector to a Hankel matrix while 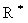 is the corresponding inverse operator.
is the corresponding inverse operator.
The final loss function is
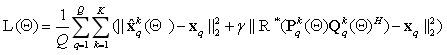 ,
,
where 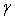 is the regularization parameter. Subscript q means the q-th index in training data of the total Q sampling trail.
is the regularization parameter. Subscript q means the q-th index in training data of the total Q sampling trail.  is the learnable network parameters including all the learnable weights of convolution layers and batch normalization layers in P and Q updating module.
is the learnable network parameters including all the learnable weights of convolution layers and batch normalization layers in P and Q updating module.
Main Results:
We evaluate the performance of the proposed DHMF on both synthetic exponential signals and realistic biological NMR spectroscopy with three state-of-the-art approaches, including LRHM [8], LRHMF [10], and DLNMR [14]. Both LRHM and LRHMF are typical model-based iterative algorithms,DLNMR is a state-of-the-art deep learning method for exponential signal reconstruction.
1. Network Interpretation
Fig.2 imply that DHMF implicitly learns the approximation of low rank property, and can provide a better interpretation of the reconstruction in the network.
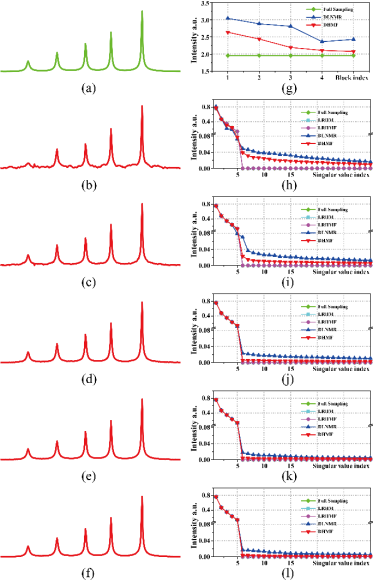
Fig. 2. The reconstructed spectra and singular values at each block. (a) fully sampled spectrum, (b)-(f) the reconstructed spectrum by the 1st to 5th blocks, (g) the nuclear norm of Hankel matrix of time domain signal, and (h)-(l) denote corresponding singular values of the ouput of each block.
2. Reconstruction of Synthetic Data
Fig.3 shows that DHMF can reconstruct signals that have a larger number of exponentials or with fewer samples. Fig.4 shows that DHMF provides the most consistent spectral peak shape and intensity, and significantly possesses the highest correlation on the weakest peak and better performance on another low-intensity peak.

Fig. 3. Average reconstruction error, RLNE, for the synthetic signal. (a) LRHM, (b)LRHMF, (c) DLNMR, (d)DHMF. Note: Each color reflects the average RLNEs over 100 Monte Carlo trials of undersamplings. Red (or white) line indicates an empirical boundary where the threshold of reconstruction error, RLNE, is 0.1 (or 0.2). The reconstruction error in the upper region above (or lower region below) the boundary is greater (or lower) than the threshold. The DLNMR did not obtain any smaller reconstruction error than 0.1 thus the region below the red line is empty.
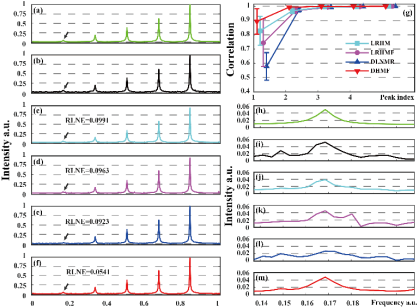
Fig. 4. Reconstructed synthetic signals with low-intensity peaks. (a) is the fully sampled noise-free signal, (b) is the noisy data with the additive Gaussian noise under standard deviation of 0.05, (c-f) are reconstructions obtained by LRHM, LRHMF, DLNMR, and DHMF from 25% data, respectively, (h-m) are the zoomed in weakest peaks marked by the arrow. (g) is the Pearsons linear correlation coefficient of each peak.
3. Reconstruction of Realistic NMR Data
Experiments on one 1H-15N TROSY spectrum (Fig. 5(a)) and one 1H-15N HSQC spectrum (Fig. 6(a)) show that DHMF provides the most faithful reconstruction for the realistic NMR spectra.
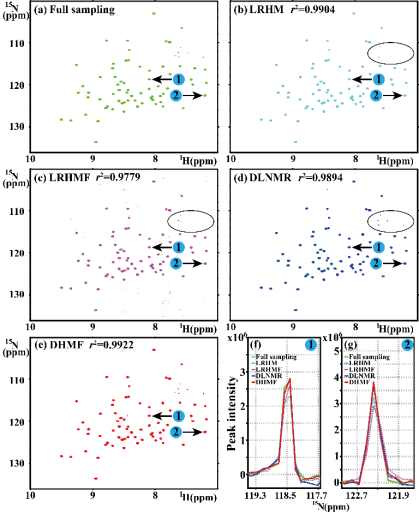
Fig. 5. The reconstruction of 2D 1H-15N TROSY spectrum of Ubiquitin. (a) is the fully sampled NMR spectrum, (b)-(e) are the reconstructions by LRHM, LRHMF, DLNMR, and DHMF, respectively. The ppm denotes parts per million by frequency, which is the unit of chemical shift.. (f) and (g) are zoomed out 1D 15N traces. Note: The data size is 127×512 and undersampling is performed on the dimension of 127 at sampling rate 25%. Note: The peak intensity correlations r2 are added in the corresponding spectra.
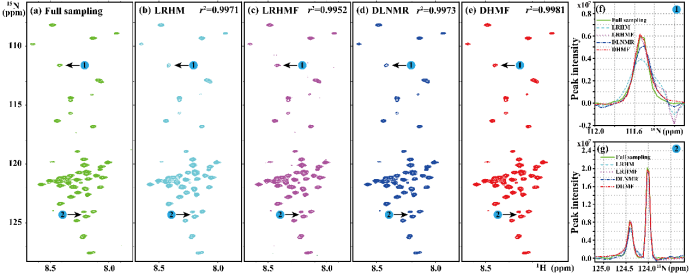
Fig. 6. The reconstruction of 2D 1H-15N HSQC spectrum of protain. (a) is the fully sampled NMR spectrum, (b)-(e) are the reconstructions by LRHM, LRHMF, DLNMR, and DHMF, respectively. (f) and (g) are zoomed out 1D 15N traces. Note: The data size is 255×116 and the undersampling is performed on the dimension of 255 at sampling rate 25%. Note: The peak intensity correlations r2 are added in the corresponding spectra.
Download:
Dataset:
Training dataset, synthetic data, and non-uniformly sampled realistic NMR data can be download here.
Paper:
Arxiv: https://arxiv.org/abs/2007.06246
Citation:
Yihui Huang, Jinkui Zhao, Zi Wang, Di Guo, Xiaobo Qu. “Complex exponential signal recovery with deep hankel matrix factorization,” arXiv preprint, arXiv:2007.06246, 2020.
Acknowledgments:
1) Data and hardware Provider
The authors would like to thank Vladislav Orekhov and Maxim Mayzel for sharing the NMR data and the GPU donated by NVIDIA Corporation. The authors thank the China Mobile Group for providing e-Cloud service. The authors thank China Mobile Group for providing e-Cloud service.
2) Fund
This work was supported in part by the National Natural Science Foundation of China (61971361, 61871341, and 61811530021), the National Key R&D Program of China (2017YFC0108703), and Xiamen University Nanqiang Outstanding Talents Program.
References:
[1] A. Hirose and S. Yoshida, "Generalization characteristics of complexvalued feedforward neural networks in relation to signal coherence," IEEE Trans. Neural Netw. Learn. Syst., vol. 23, no. 4, pp. 541-551, 2012.
[2] C. Qian, L. Huang, M. Cao, J. Xie, and H. C. So, "PUMA: An improved realization of MODE for DOA estimation," IEEE Trans. Aerosp. Electron. Syst., vol. 53, no. 5, pp. 2128-2139, 2017.
[3] D. Nion and N. D. Sidiropoulos, "Tensor algebra and multidimensional harmonic retrieval in signal processing for mimo radar," IEEE Trans. Signal Process., vol. 58, no. 11, pp. 5693-5705, 2010.
[4] L. Schermelleh, R. Heintzmann, and H. Leonhardt, "A guide to superresolution fluorescence microscopy," J. Cell Biol., vol. 190, no. 2, pp. 165-175, 2010.
[5] J. A. Tropp, J. N. Laska, M. F. Duarte, J. K. Romberg, and R. G. Baraniuk, "Beyond Nyquist: Efficient sampling of sparse bandlimited signals," IEEE Trans. Inf. Theory, vol. 56, no. 1, pp. 520-544, 2010.
[6] M. Vetterli, P. Marziliano, and T. Blu, "Sampling signals with finite rate of innovation," IEEE Trans. Signal Process., vol. 50, no. 6, pp. 1417-1428, 2002.
[7] M. Elad, P. Milanfar, and G. Golub, H, "Shape from moments – an estimation theory perspective," IEEE Trans. Signal Process., vol. 52, no. 7, pp. 1814-1829, 2004.
[8] X. Qu, M. Mayzel, J.-F. Cai, Z. Chen, and V. Orekhov, "Accelerated NMR spectroscopy with low-rank reconstruction," Angew. Chem.-Int. Edit., vol.54, no. 3, pp. 852-854, 2015.
[9] H. M. Nguyen, X. Peng, M. N. Do, and Z.-P. Liang, "Denoising MR spectroscopic imaging data with low-rank approximations," IEEE Trans. Biomed. Eng., vol. 60, no. 1, pp. 78-89, 2013.
[10] D. Guo, H. Lu, and X. Qu, "A fast low rank Hankel matrix factorization reconstruction method for non-uniformly sampled magnetic resonance spectroscopy," IEEE Access, vol. 5, pp. 16033-16039, 2017.
[11] J. Ying, H. Lu, Q. Wei, J.-F. Cai, D. Guo, J. Wu, Z. Chen, and X. Qu, "Hankel matrix nuclear norm regularized tensor completion for Ndimensional exponential signals," IEEE Trans. Signal Process., vol. 65, no.14, pp. 3702-3717, 2017.
[12] H. Lu, X. Zhang, T. Qiu, J. Yang, J. Ying, D. Guo, Z. Chen, and X. Qu, "Low rank enhanced matrix recovery of hybrid time and frequency data in fast magnetic resonance spectroscopy," IEEE Trans. Biomed. Eng., vol. 65, no. 4, pp. 809-820, 2018.
[13] H. Cai, J. Cai, T. Wang, and G. Yin, "Accelerated structured alternating projections for robust spectrally sparse signal recovery," IEEE Trans. Signal Process., vol. 69, pp. 809-821, 2021.
[14] X. Qu, Y. Huang, H. Lu, T. Qiu, D. Guo, T. Agback, V. Orekhov, and Z.Chen, "Accelerated nuclear magnetic resonance spectroscopy with deep learning," Angew. Chem.-Int. Edit., vol. 59, no. 26, pp. 10297-10300, 2020.
[15] K. Usevich and P. Comon, "Hankel low-rank matrix completion: Performance of the nuclear norm relaxation," IEEE J. Sel. Top. Signal Process., vol. 10, no. 4, pp. 637-646, 2016.
[16] Y. Chen and Y. Chi, "Robust spectral compressed sensing via structured matrix completion," IEEE Trans. Inf. Theory, vol. 60, no. 10, pp. 6576-6601, 2014.
[17] J. Ying, J.-F. Cai, D. Guo, G. Tang, Z. Chen, and X. Qu, "Vandermonde factorization of Hankel matrix for complex exponential signal recovery—application in fast NMR spectroscopy," IEEE Trans. Signal Process., vol.66, no. 21, pp. 5520-5533, 2018.
[18] K. Kazimierczuk and V. Y. Orekhov, "Accelerated NMR spectroscopy by using compressed sensing," Angew. Chem.-Int. Edit., vol. 50, no. 24, pp.5556-5559, 2011.
[19] X. Qu, X. Cao, D. Guo, and Z. Chen, "Compressed sensing for sparse magnetic resonance spectroscopy," in Int. Soc. Magn. Reson. Med. 18th Sci.Meet., 2010, p. 3371.
[20] D. J. Holland, M. J. Bostock, L. F. Gladden, and D. Nietlispach, "Fast multidimensional NMR spectroscopy using compressed sensing," Angew.Chem.-Int. Edit., vol. 50, no. 29, pp. 6548-6551, 2011.
[21] S. G. Hyberts, K. Takeuchi, and G. Wagner, "Poisson-gap sampling and forward maximum entropy reconstruction for enhancing the resolution and sensitivity of protein NMR data," J. Am. Chem. Soc., vol. 132, no. 7, pp.2145-2147, 2010.
[22] X. Qu, D. Guo, X. Cao, S. Cai, and Z. Chen, "Reconstruction of self-sparse 2d NMR spectra from under sampled data in the indirect dimension,"Sensors, vol. 11, no. 9, pp. 8888-8909, 2011.
[23] Z. Tu, H. Liu, J. Zhan, and D. Guo, "A fast self-learning subspace reconstruction method for non-uniformly sampled nuclear magnetic resonance spectroscopy," Applied Sciences, vol. 10, no. 11, p. 3939, 2020.
[24] E. J. Candès, J. Romberg, and T. Tao, "Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information,"IEEE Trans. Inf. Theory, vol. 52, no. 2, pp. 489-509, 2006.
[25] V. Chandrasekaran, B. Recht, P. A. Parrilo, and A. S. Willsky, "The convex geometry of linear inverse problems," Found. Comput. Math., vol. 12, no.6, pp. 805-849, 2012.
[26] T. Qiu, Z. Wang, H. Liu, D. Guo, and X. Qu, "Review and prospect: NMR spectroscopy denoising and reconstruction with low-rank Hankel matrices and tensors," Magnetic Resonance in Chemistry, vol. 59, no. 3, pp. 324-345, 2021.
[27] J.-M. Papy, L. De Lathauwer, and S. Van Huffel, "Exponential data fitting using multilinear algebra: The decimative case," J. Chemometr., vol. 23, no. 7‐8, pp. 341-351, 2009.
[28] M. Fazel, T. K. Pong, D. Sun, and P. Tseng, "Hankel matrix rank minimization with applications to system identification and realization,"SIAM J. Matrix Anal. Appl., vol. 34, no. 3, pp. 946-977, 2013.
[29] I. Markovsky, "Recent progress on variable projection methods for structured low-rank approximation," Signal Process., vol. 96, pp. 406-419, 2014.
[30] J.-F. Cai, X. Qu, W. Xu, and G. Ye, "Robust recovery of complex exponential signals from random Gaussian projections via low rank Hankel matrix reconstruction," Appl. Comput. Harmon. Anal., vol. 41, no. 2, pp.470-490, 2016.
[31] I. Markovsky and K. Usevich, "Structured low-rank approximation with missing data," SIAM J. Matrix Anal. Appl., vol. 34, no. 2, pp. 814-830, 2013.
[32] X. Peng, C. Lu, Z. Yi, and H. Tang, "Connections between nuclear-norm and Frobenius-norm-based representations," IEEE Trans. Neural Netw.Learn. Syst., vol. 29, no. 1, pp. 218-224, 2018.
[33] J.-F. Cai, E. J. Candes, and Z. Shen, "A singular value thresholding algorithm for matrix completion," SIAM J. Optim., vol. 20, no. 4, pp. 1956-1982, 2010.
[34] K. H. Jin, D. Lee, and J. C. Ye, "A general framework for compressed sensing and parallel MRI using annihilating filter based low-rank Hankel matrix," IEEE Trans. Comput. Imaging, vol. 2, no. 4, pp. 480-495, 2016.
[35] X. Zhang, D. Guo, Y. Huang, Y. Chen, L. Wang, F. Huang, Q. Xu, and X.Qu, "Image reconstruction with low-rankness and self-consistency of kspace data in parallel MRI," Med. Image Anal., vol. 63, p. 101687, 2020.
[36] Y. LeCun, Y. Bengio, and G. Hinton, "Deep learning," Nature, vol. 521, no. 7553, pp. 436-444, 2015.
[37] R. Liu, Z. Jiang, X. Fan, and Z. Luo, "Knowledge-driven deep unrolling for robust image layer separation," IEEE Trans. Neural Netw. Learn. Syst., vol. 31, no. 5, pp. 1653-1666, 2020.
[38] D. Chen, Z. Wang, D. Guo, V. Orekhov, and X. Qu, "Review and prospect: Deep learning in nuclear magnetic resonance spectroscopy," Chem.-Eur. J., vol. 26, pp. 10391-10401, 2020.
[39] Y. Yang, J. Sun, H. Li, and Z. Xu, "ADMM-CSNet: A deep learning approach for image compressive sensing," IEEE Trans. Pattern Anal.Mach. Intell., vol. 42, pp. 521-538, 2020.
[40] T. Lu, X. Zhang, Y. Huang, D. Guo, F. Huang, Q. Xu, Y. Hu, L. Ou-Yang, J. Lin, Z. Yan, and X. Qu, "pFISTA-SENSE-ResNet for parallel MRI reconstruction," J. Magn. Reson., vol. 318, p. 106790, 2020, Art no.106790.
[41] V. Monga, Y. Li, and C. Elda, Yonina, "Algorithm unrolling: Interpretable, efficient deep learning for signal and image processing," IEEE Signal Process. Mag., vol. 38, no. 2, pp. 18-44, 2021.
[42] J. Zhang and B. Ghanem, "ISTA-Net: Interpretable optimization-inspired deep network for image compressive sensing," in Proc. CVPR, 2018, pp.1828-1837.
[43] S. Gunasekar, B. Woodworth, S. Bhojanapalli, B. Neyshabur, and N.Srebro, "Implicit regularization in matrix factorization," in Proc. NIPS, 2017, vol. 30, pp. 6151-6159.
[44] S. Arora, N. Cohen, W. Hu, and Y. Luo, "Implicit regularization in deep matrix factorization," in Proc. NIPS, 2019, vol. 32, pp. 7413-7424.
[45] G. Trigeorgis, K. Bousmalis, S. Zafeiriou, and B. W. Schuller, "A deep matrix factorization method for learning attribute representations," IEEE Trans. Pattern Anal. Mach. Intell., vol. 39, no. 3, pp. 417-429, 2017.
[46] X.-R. Feng, H.-C. Li, J. Li, Q. Du, A. Plaza, and J. Emery, William; , "Hyperspectral unmixing using sparsity-constrained deep nonnegative matrix factorization with total variation," IEEE Trans. Geosci. Remote Sensing, vol. 56, no. 10, pp. 6245-6257, 2018.
[47] P. Sprechmann, A. M. Bronstein, and G. Sapiro, "Learning efficient sparse and low rank models," IEEE Trans. Pattern Anal. Mach. Intell., vol. 37, no.9, pp. 1821-1833, 2015.
[48] O. Solomon, R. Cohen, Y. Zhang, Y. Yang, Q. He, J. Luo, R. J. G. v. Sloun, and Y. C. Eldar, "Deep unfolded robust PCA with application to clutter suppression in ultrasound," IEEE Trans. Med. Imaging, vol. 39, no. 4, pp.1051-1063, 2020.
[49] N. Srebro, "Learning with matrix factorizations," Ph.D. dissertation, MIT, 2004.
[50] S. Boyd, N. Parikh, E. Chu, B. Peleato, and J. Eckstein, "Distributed optimization and statistical learning via the alternating direction method of multipliers," Found. Trends Mach. Learn., vol. 3, no. 1, pp. 1-122, 2011.
[51] G. Huang, Z. Liu, L. Van Der Maaten, and K. Q. Weinberger, "Densely connected convolutional networks," in Proc. CVPR, 2017, pp. 4700-4708.
[52] W. Lee, M. Tonelli, and J. L. Markley, "NMRFAM-SPARKY: Enhanced software for biomolecular NMR spectroscopy," Bioinformatics, vol. 31, no.8, pp. 1325-1327, 2015.
[53] D. P. Kingma and J. Ba, "Adam: A method for stochastic optimization," arXiv Preprint arXiv:1412.6980, 2014.
[54] F. Delaglio, S. Grzesiek, G. W. Vuister, G. Zhu, J. Pfeifer, and A. Bax, "NMRPipe: A multidimensional spectral processing system based on UNIX pipes," J. Biomol. NMR, vol. 6, no. 3, pp. 277-293, 1995.
[55] J. C. Hoch and A. S. Stern, NMR Data Processing. Wiley, 1996.
[56] R. Roy and T. Kailath, "ESPRIT-estimation of signal parameters via rotational invariance techniques," IEEE Trans. Acoust., Speech, Signal Process., vol. 37, no. 7, pp. 984-995, 1989.
[57]P. Stoica and R. L. Moses, Spectral Analysis of Signals. Prentice Hall, 2005

![]() block are designed as:
block are designed as: 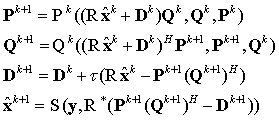
![]() and
and ![]() are updating operators,
are updating operators, ![]() denotes the data consistency operator,
denotes the data consistency operator, ![]() is the learning step,
is the learning step, ![]() denotes the Hankel operator mapping the vector to a Hankel matrix while
denotes the Hankel operator mapping the vector to a Hankel matrix while ![]() is the corresponding inverse operator.
is the corresponding inverse operator.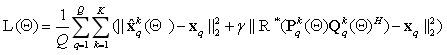 ,
,![]() is the regularization parameter. Subscript q means the q-th index in training data of the total Q sampling trail.
is the regularization parameter. Subscript q means the q-th index in training data of the total Q sampling trail. ![]() is the learnable network parameters including all the learnable weights of convolution layers and batch normalization layers in P and Q updating module.
is the learnable network parameters including all the learnable weights of convolution layers and batch normalization layers in P and Q updating module.



