并行磁共振成像重建中投影快速迭代软阈值算法的收敛性分析

并行磁共振成像重建中投影快速迭代软阈值算法的收敛性分析 (中文，English)

张心林¹, 鲁恒发¹, 郭迪², 包立君¹, 黄峰³, 徐勤³, 屈小波^1,*

¹ 厦门大学，电子科学系，福建等离子体与磁共振重点研究实验室，中国，厦门，361005.
² 厦门理工学院，计算机与信息工程学院，中国，厦门，361024.
³ 东软医疗系统有限公司，中国，上海，200241.
^* Emails: quxiaobo <at> xmu.edu.cn or quxiaobo2009 <at> gmail.com

引用

Xinlin Zhang, Hengfa Lu, Di Guo, Lijun Bao, Feng Huang, Qin Xu, Xiaobo Qu, A Guaranteed Convergence Analysis for the Projected Fast Iterative Soft-thresholding Algorithm in Parallel MRI, Medical Image Analysis, 69: 101987, 2021.

摘要

稀疏采样和并行成像技术是缓解磁共振成像 (Magnetic resonance imaging, MRI)采集时间过长问题的有效手段。借助稀疏重建，我们可以从稀疏采样的少量数据中恢复出完整的图像。在稀疏重建中，选择合适的算法对重建模型求解是至关重要的。投影快速迭代软阈值算法（Projected fast iterative soft-thresholding algorithm, pFISTA）是一种简单高效的算法，已成功扩展到并行成像。然而，pFISTA在并行成像中的收敛准则仍然是一个未解决的问题，现有的单通道pFISTA收敛条件不适用于并行成像pFISTA，这使得用户难以选择一个合适的算法参数，既能保证收敛，又能快速完成重建。
本工作中，我们证明并分析了并行成像中pFISTA的收敛性，给出了使用pFISTA求解SENSE和SPIRiT重建的推荐参数。实测数据结果表明：使用本文收敛性分析推荐的步长可以以最快的速度重建出可靠的图像。这项工作将有望帮助用户快速选择步长以获得可靠的重建结果和快速的收敛速度，并促进稀疏机器学习重建在并行MRI中的应用。

方法

1. 背景

磁共振成像（Magnetic resonance imaging, MRI）是一种非侵入性、非放射性的成像技术，是医学诊断中广泛采用和不可或缺的工具。然而，缓慢的成像速度限制了其应用。稀疏采样和并行成像技术是加速 MRI 采集的有效方法。通过稀疏重建，我们可以从少量数据点中恢复图像。在稀疏重建方法中，选择合适的算法来求解重建模型非常重要。
针对单通道MRI重建，我们小组提出了投影快速迭代软阈值算法（Projected fast iterative soft-thresholding algorithm, pFISTA），该算法能够实现更快的重建，需要更少的内存空间，并且只有一个可调参数，步长$\gamma$。同时，我们证明了单通道重建下pFISTA的收敛条件，这能够极大地减少用户调节参数的时间，提高数据采集和重建过程的效率。
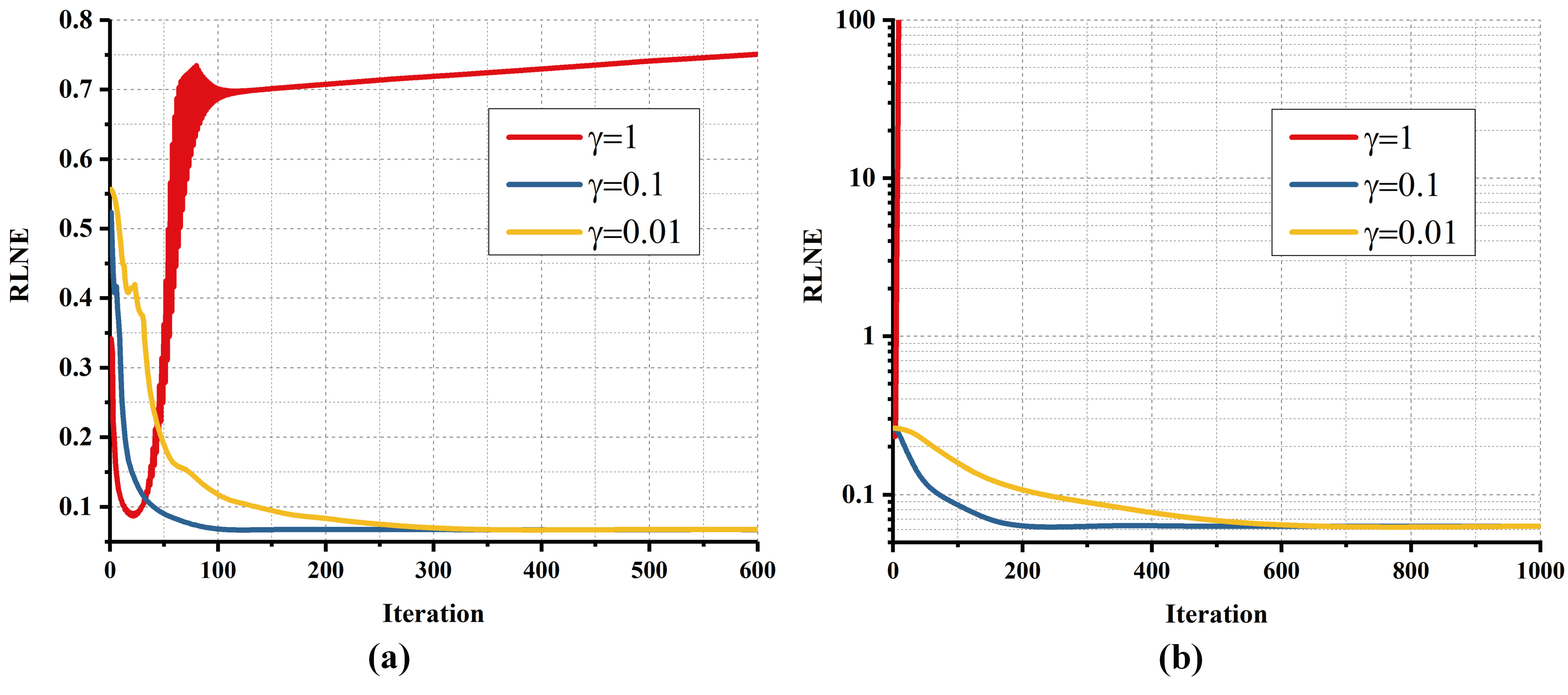
最近，pFISTA成功应用于并行成像MRI重建。然而，pFISTA在并行成像中的收敛性仍未被证明。单通道pFISTA的收敛条件不能直接应用于并行成像pFISTA。如图 1所示，过大的$\gamma$会导致算法不收敛，而过小的$\gamma$使得重建速度变慢。因此，用户将会面临如何选择合适的 $\gamma$的问题，以达到快速可靠的重建。

图 1. pFISTA-SENSE(a)以及pFISTA-SPIRiT(b)的经验收敛性。注：实验为3倍加速的32通道实测MRI图像重建。

2. 基于pFISTA算法的并行MRI重建

并行MRI重建可以大致分为两类：图像域重建方法，如SENSE（sensitivity encoding）；以及k空间重建方法，如SPIRiT（iterative self-consistent parallel imaging reconstruction）。我们可以将这两类并行 MRI 重建问题用统一的形式表达：

$$ \mathop {\min }\limits_{\mathbf{d}} \lambda {\left\| {{\mathbf{\Psi d}}} \right\|_1} + \frac{1}{2} \left\| {{\mathbf{y}} - {\mathbf{Ad}}} \right\|_2^2, $$ 这里$\mathbf{d}$表示待重建的图像，$\mathbf{y}=\left[ {{\mathbf{y}}_{1}};{{\mathbf{y}}_{2}};\cdots ;{{\mathbf{y}}_{J}} \right] \in{\mathbb{C}^{MJ}}$表示排列成列向量的采样得到的多通道数据，${{\mathbf{y}}_{j}}\in{\mathbb{C}^{M}} \;\left( j=1,2,\cdots ,J \right)$表示采样到的第$j$个通道内的k空间数据,$\mathbf{A}$表示并行MRI的系统矩阵，包含了通道调制、傅里叶变换以及欠采样。$\mathbf{\Psi }$是一个紧标架，常数$\lambda $是用于平衡稀疏项和数据校验项的正则化参数。为简单起见，我们将用于解决并行MRI重建的pFISTA算法称为pFISTA-parallel。
用pFISTA算法求解上述并行MRI重建问题的主要迭代步骤包括： $$ {\mathbf{d}}^{\left( {k + 1} \right)} = {{\mathbf{\Psi }}^*}{T_{\gamma \lambda }} \left( {{\mathbf{\Psi }} \left( {\hat{\mathbf{d}}^{\left( k \right)} + \gamma {{\mathbf{A}}^H} \left( {{{\mathbf{y}}} - {\mathbf{A}\hat{\mathbf{d}}}^{\left( k \right)}} \right)} \right)} \! \right), $$ $$ {t^{\left( {k + 1} \right)}} = \frac{{1 + \sqrt {1 + 4{{\left( {{t^{\left( k \right)}}} \right)}^2}} }}{2}, $$ $$ {\hat{\mathbf{d}}}^{\left( {k + 1} \right)} = {\mathbf{d}}^{\left( {k + 1} \right)} + \frac{{{t^{\left( {k} \right)}} - 1}}{t^{\left( {k + 1} \right)}}\left( {{\mathbf{d}}^{\left( {k + 1} \right)} - {\mathbf{d}}^{\left( k \right)}} \right), $$ 这里${{T}_{\gamma \lambda }}\left( \cdot \right)$是软阈值算子，上标$H$表示矩阵的共轭转置。
在这项工作中，我们证明了pFISTA-parallel的收敛性，给出了基于SENSE和基于SPIRiT的pFISTA并行MRI重建的推荐参数。并行成像pFISTA的收敛条件：
设$\left\{ \mathbf{d}^{\left(k \right)} \right\}$是由pFISTA-parallel生成的一串数列，当步长满足$\gamma \le 1/c$，同时$\mathbf{\Psi }$是一个紧标架时，pFISTA-parallel算法收敛。这里，$c$ 是与线圈相关的常数，可以在从重建之前通过自动校准信号计算出来。

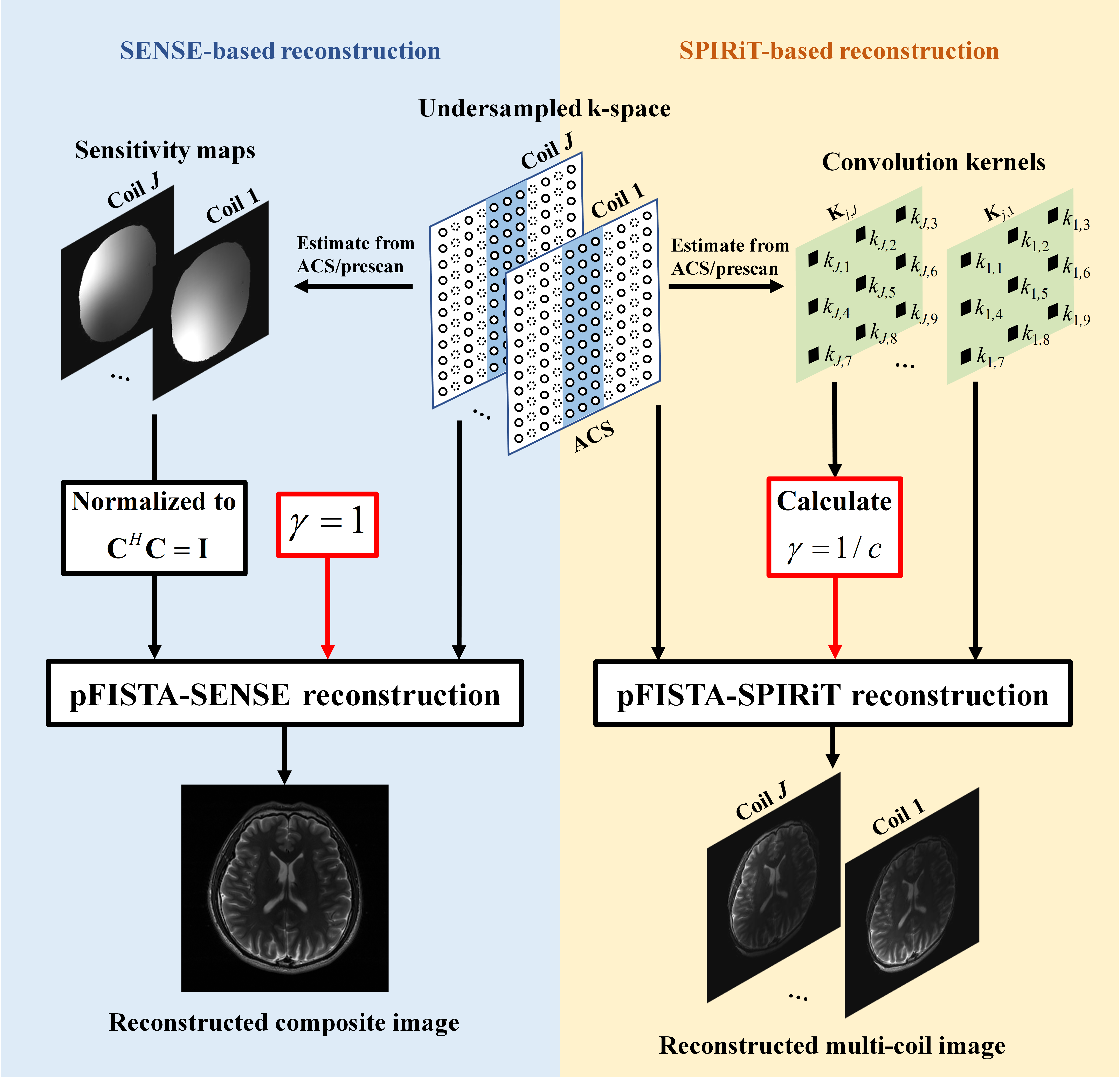
图 2. pFISTA-parallel 的重建流程示意图。。

3. 主要结果

我们使用了三组实测数据（通道数分别为8、12和32）进行实验。实验将测试3倍加速下的重建结果，采用相对二范数误差(Relative L2-norm error, RLNE)作为指标来评价重建的结果，RLNE越低，则表示重建图像与原图之间的误差越小。
如图3所示，使用本文收敛性分析推荐的步长可以以最快的速度重建出图像，重建图像误差低。这项工作将有望帮助用户快速选择步长以获得可靠的重建结果和快速的收敛速度，并促进稀疏机器学习重建在并行MRI中的应用。

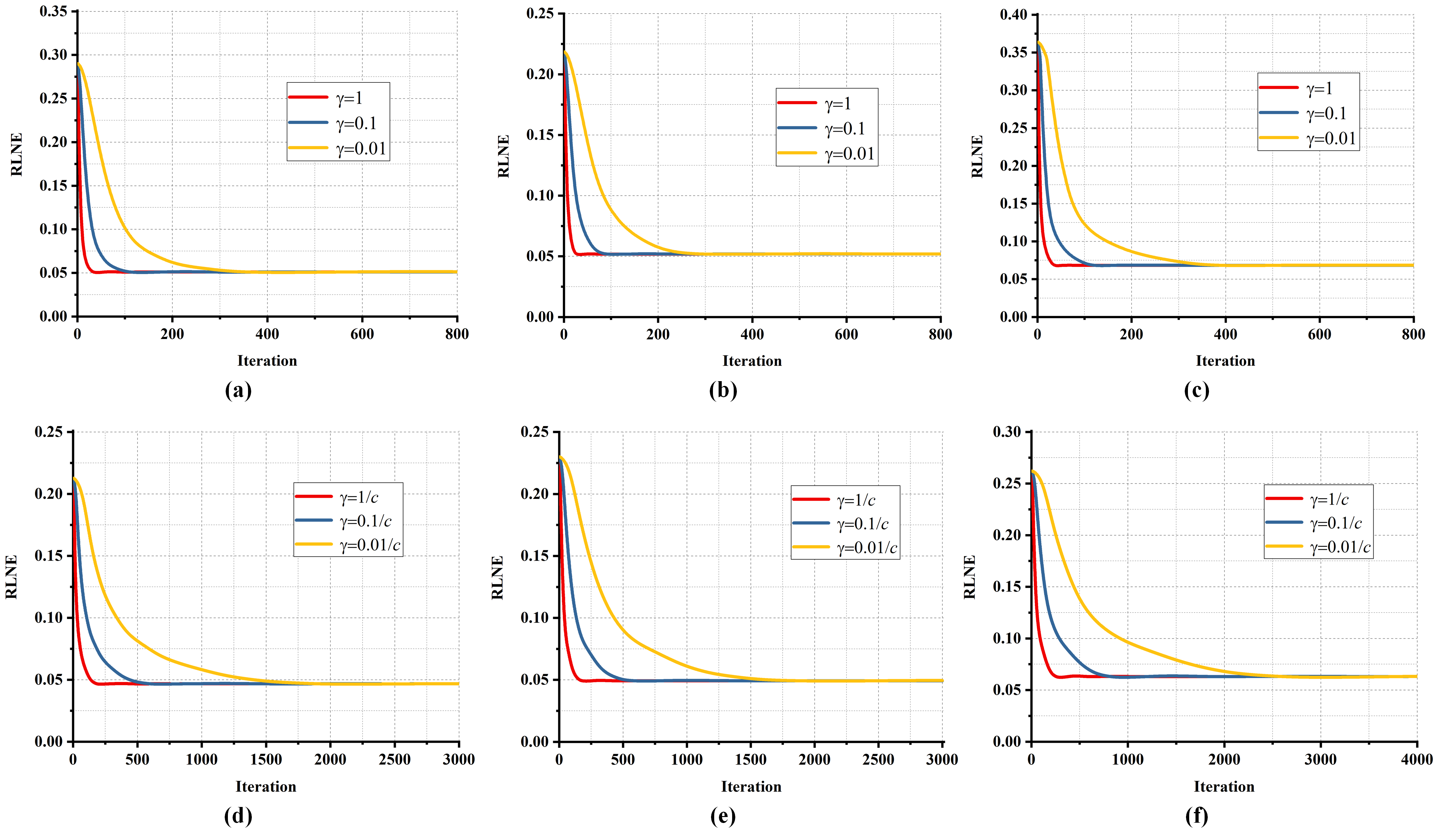
3倍加速下的pFISTA-parallel重建的经验收敛性。(a-c)分别是8、12、32通道数据的pFISTA-SENSE的收敛性。(d-f)分别是8、12、32通道数据的pFISTA-SPIRiT的收敛性。

代码下载

所提方法的MATLAB代码可以从这里下载。

致谢

这项工作得到了国家重点研发计划（2017YFC0108700），国家自然科学基金（61971361、61871341、61811530021、U1632274和61672335），福建省自然科学基金（2018J06018），中央高校基本科研基金（20720180056），和厦门大学南强拔尖人才计划的资助。

参考文献:

[1] J. Hamilton et al., “Recent advances in parallel imaging for MRI,” Progress in Nuclear Magnetic Resonance Spectroscopy, vol. 101, pp. 71–95, 2017.
[2] M. Lustig, et al., "Sparse MRI: the application of compressed sensing for rapid MR imaging," Magnetic Resonance Medicine, vol. 58, no. 6, pp. 1182–1195, 2007.
[3] K. P. Pruessmann et al., “SENSE: Sensitivity encoding for fast MRI,” Magnetic Resonance in Medicine, vol. 42, pp. 952–962, 1999.
[4] M. Lustig and J. M. Pauly, "SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-space," Magnetic Resonance in Medicine, vol. 64, no. 2, pp. 457-471, 2010.
[5] Y. Liu, et al., "Balanced sparse model for tight frames in compressed sensing magnetic resonance imaging," PLoS One, vol. 10, no. 4, p. e0119584, 2015.
[6] Y. Liu, et al., "Projected iterative soft-thresholding algorithm for tight frames in compressed sensing magnetic resonance imaging," IEEE Transaction on Medical Imaging, vol. 35, no. 9, pp. 2130–2140, 2016.
[7] S.T. Ting, et al., "Fast implementation for compressive recovery of highly accelerated cardiac cine MRI using the balanced sparse model," Magnetic Resonance in Medicine, vol. 77, no. 4, pp. 1505–1515, 2017.
[8] Y. Hu, et al., "Spatiotemporal flexible sparse reconstruction for rapid dynamic contrast-enhanced MRI," IEEE Transactions on Biomedical Engineering, doi: 10.1109/TBME.2021.3091881, 2021.