A Guaranteed Convergence Analysis for the Projected Fast Iterative Soft-thresholding Algorithm in Parallel MRI

A Guaranteed Convergence Analysis for the Projected Fast Iterative Soft-thresholding Algorithm in Parallel MRI (中文，English)

Xinlin Zhang¹, Hengfa Lu¹, Di Guo², Lijun Bao¹, Feng Huang³, Qin Xu³, Xiaobo Qu^1,*

¹ Department of Electronic Science, Fujian Provincial Key Laboratory of Plasma and Magnetic Resonance, School of Electronic Science and Engineering, National Model Microelectronics College, Xiamen University, Xiamen 361005, China.
² School of Computer and Information Engineering, Fujian Provincial University Key Laboratory of Internet of Things Application Technology, Xiamen University of Technology, Xiamen 361024, China.
³ Neusoft Medical System, Shanghai 200241, China.
^* Emails: quxiaobo <at> xmu.edu.cn or quxiaobo2009 <at> gmail.com

Citation

Xinlin Zhang, Hengfa Lu, Di Guo, Lijun Bao, Feng Huang, Qin Xu, Xiaobo Qu, A Guaranteed Convergence Analysis for the Projected Fast Iterative Soft-thresholding Algorithm in Parallel MRI, Medical Image Analysis, 69: 101987, 2021.

Synopsis

Sparse sampling and parallel imaging techniques are two effective approaches to alleviate the lengthy magnetic resonance imaging (MRI) data acquisition problem. Promising data recoveries can be obtained from a few MRI samples with the help of sparse reconstruction models. To solve the optimization models, proper algorithms are indispensable. The pFISTA, a simple and efficient algorithm, has been successfully extended to parallel imaging. However, its convergence criterion is still an open question. Besides, the ex- isting convergence criterion of single-coil pFISTA cannot be applied to the parallel imaging pFISTA, which, therefore, imposes confusions and difficulties on users about determining the only parameter - step size.
In this work, we provide the guaranteed convergence analysis of the parallel imaging version pFISTA to solve the two well-known parallel imaging reconstruction models, SENSE and SPIRiT. Along with the con- vergence analysis, we provide recommended step size values for SENSE and SPIRiT reconstructions to obtain fast and promising reconstructions. Experiments on in vivo brain images demonstrate the validity of the convergence criterion.

Method

1. Background

Magnetic resonance imaging (MRI) is a non-invasive, non-radioactive, and versatile technique serving as a widely adopted and indispensable tool in medical diagnosis. However, the slow imaging speed limits its applications. Sparse sampling and parallel imaging technology are effective methods to accelerate MRI acquisition. With the help of sparse reconstruction methods, we can recover an image from a small amount of data points. It is crucial to choose a suitable algorithm to solve the reconstruction model in sparse reconstruction methods.
According to the single-coil MRI reconstruction, a novel algorithm, named projected fast iterative soft-threshold algorithm (pFISTA) developed by our group, enable faster reconstructions, require less memory space and have only one adjustable parameter, the step size $\gamma$. Moreover, its convergence criterion has been provided, making it easier for users to adjust the parameter and improving the efficiency of the data acquisition and reconstruction process.
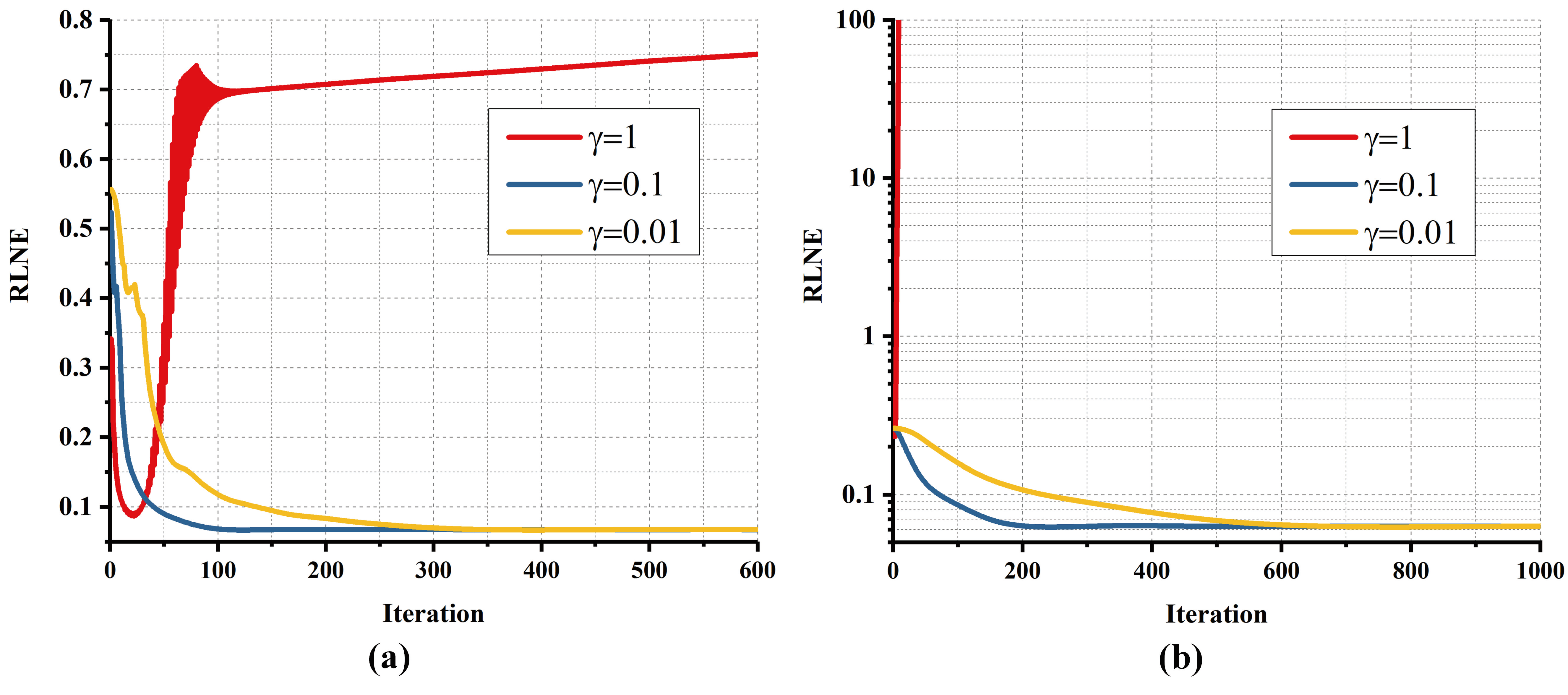
Recently, pFISTA has been successfully applied in parallel imaging reconstruction. The convergence criterion, however, is still an open question. In addition, the convergence criterion proved for the single-coil pFISTA cannot be directly applied to the multi-coil cases (Fig. 1). Therefore, the algorithm users would encounter a problem of how to choose a proper $\gamma$ to produce faithful results.

Fig. 1. Empirical convergence of pFISTA-SENSE (a) and pFISTA-SPIRiT (b) with different $\gamma$.

2. pFISTA for parallel imaging MRI reconstruction

The parallel MRI reconstruction approaches can be categorized into two main genres: Image domain methods, such as sensitivity encoding (SENSE), and k-space domain methods, e.g., iterative self-consistent parallel imaging reconstruction (SPIRiT). We can formulate analysis models for these two parallel MRI reconstruction problems into a unified form as:

$$ \mathop {\min }\limits_{\mathbf{d}} \lambda {\left\| {{\mathbf{\Psi d}}} \right\|_1} + \frac{1}{2} \left\| {{\mathbf{y}} - {\mathbf{Ad}}} \right\|_2^2, $$ where $\mathbf{d}$ represents the desired image to be recovered, $\mathbf{y}=\left[ {{\mathbf{y}}_{1}};{{\mathbf{y}}_{2}};\cdots ;{{\mathbf{y}}_{J}} \right] \in{\mathbb{C}^{MJ}}$ the undersampled multi-coil k-space data rearranged into a column vector, and ${{\mathbf{y}}_{j}}\in{\mathbb{C}^{M}} \;\left( j=1,2,\cdots ,J \right)$ is the undersampled k-space data vector of $j$-th coil, and $\mathbf{A}$ as a system matrix in parallel MRI, including coils modulation, Fourier transform, and undersampling. $\mathbf{\Psi }$ is a tight frame, and the constant $\lambda $ is the regularization parameter to balance the sparsity and data consistency. And for simplicity, we call the pFISTA adopted to solve parallel MRI reconstruction as pFISTA-parallel.
The main iteration of pFISTA to solve the problem are $$ {\mathbf{d}}^{\left( {k + 1} \right)} = {{\mathbf{\Psi }}^*}{T_{\gamma \lambda }} \left( {{\mathbf{\Psi }} \left( {\hat{\mathbf{d}}^{\left( k \right)} + \gamma {{\mathbf{A}}^H} \left( {{{\mathbf{y}}} - {\mathbf{A}\hat{\mathbf{d}}}^{\left( k \right)}} \right)} \right)} \! \right), $$ $$ {t^{\left( {k + 1} \right)}} = \frac{{1 + \sqrt {1 + 4{{\left( {{t^{\left( k \right)}}} \right)}^2}} }}{2}, $$ $$ {\hat{\mathbf{d}}}^{\left( {k + 1} \right)} = {\mathbf{d}}^{\left( {k + 1} \right)} + \frac{{{t^{\left( {k} \right)}} - 1}}{t^{\left( {k + 1} \right)}}\left( {{\mathbf{d}}^{\left( {k + 1} \right)} - {\mathbf{d}}^{\left( k \right)}} \right), $$ where ${{T}_{\gamma \lambda }}\left( \cdot \right)$ is a point-wise soft-thresholding function, and the superscript $H$ denotes the conjugate transpose of a matrix.
In this work, we prove the convergence of pFISTA-parallel, and offer recommended step sizes for pFISTA under both SENSE-based and SPIRiT-based reconstruction. The convergence of pFISTA-parallel can be summarized in the form of a theorem:
Let $\left\{ \mathbf{d}^{\left(k \right)} \right\}$ be generated by pFISTA-parallel, the step size satisfies $\gamma \le 1/c$, and $\mathbf{\Psi }$ is a tight frame, the pFISTA-parallel algorithm converges. Here, $c$ is a constant related to the coils and can be calculated before reconstruction from the auto-calibration signal.

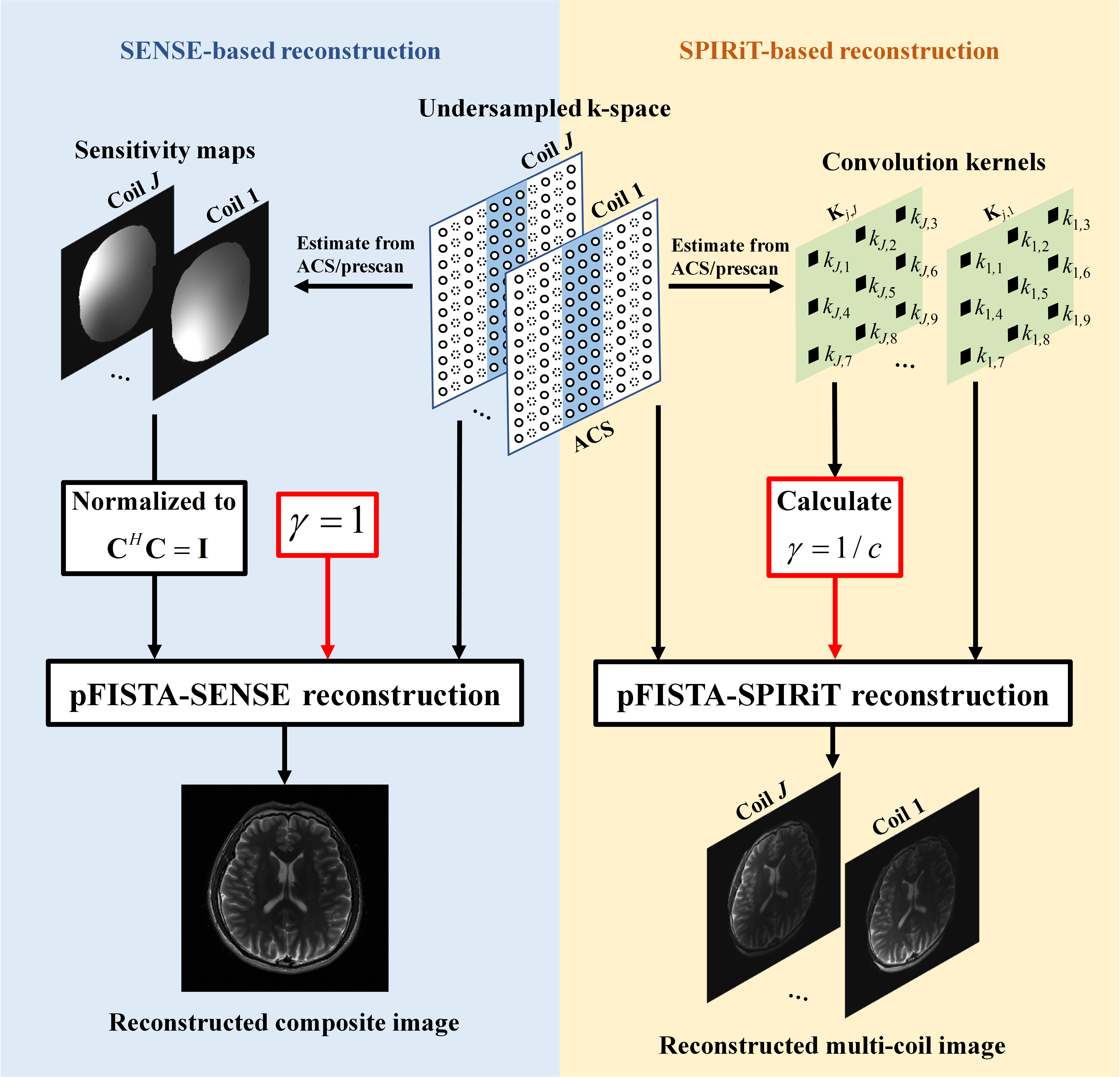
Fig. 2. A pipeline flowchart of pFISTA-parallel reconstruction.

3. Main result

Three different datasets (8-, 12-, and 32-coil) in vivo human brain MRI data was adopted in experiments, and the acceleration factor equals 3. We adopt relative L2 norm error (RLNE) as objective criteria to quantify the reconstruction performance. A lower RLNE demonstrates higher consistency between the fully sampled image and the reconstructed image.
Experimental results evince the validity and effectiveness of the convergence criterion (Fig. 3). This work is expected to help users quickly choose the step size to obtain faithful results and fast convergence speed and to promote the application of sparse reconstruction in parallel MRI.

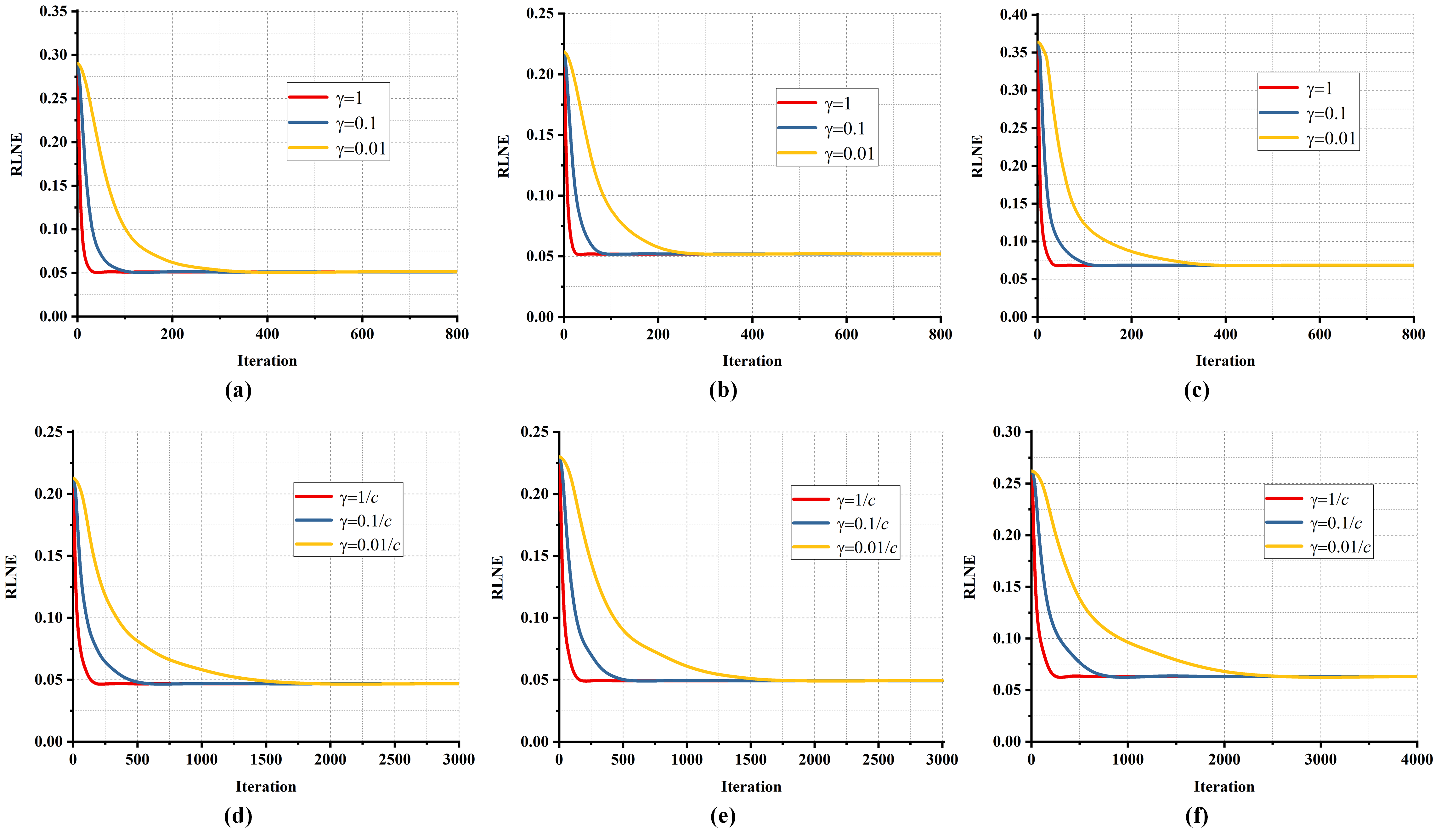
Empirical convergence results of pFISTA-parallel reconstruction under $3 times$ acceleration. (a-c) are the convergence results of pFISTA-SENSE for 8, 12, and 32 channel data respectively. (d-f) are the convergence results of pFISTA-SPIRiT for 8, 12, and 32 channel data respectively。

Code

The MATLAB code of pFISTA-parallel can be downloaded here.

Acknowledgments

This work was supported in part by National Key R&D Program of China ( 2017YFC0108703 ), National Natural Science Foundation of China ( 61971361 , 61871341 , 61811530021 , U1632274 and 61672335 ), Natural Science Foundation of Fujian Province of China (2018J06018), Fundamental Research Funds for the Central Universities (20720180056 and 20720200065), Health-Education Joint Research Project of Fujian Province (2019-WJ-31), and Xiamen University Nanqiang Outstanding Talents Program.

References:

[1] J. Hamilton et al., “Recent advances in parallel imaging for MRI,” Progress in Nuclear Magnetic Resonance Spectroscopy, vol. 101, pp. 71–95, 2017.
[2] M. Lustig, et al., "Sparse MRI: the application of compressed sensing for rapid MR imaging," Magnetic Resonance Medicine, vol. 58, no. 6, pp. 1182–1195, 2007.
[3] K. P. Pruessmann et al., “SENSE: Sensitivity encoding for fast MRI,” Magnetic Resonance in Medicine, vol. 42, pp. 952–962, 1999.
[4] M. Lustig and J. M. Pauly, "SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-space," Magnetic Resonance in Medicine, vol. 64, no. 2, pp. 457-471, 2010.
[5] Y. Liu, et al., "Balanced sparse model for tight frames in compressed sensing magnetic resonance imaging," PLoS One, vol. 10, no. 4, p. e0119584, 2015.
[6] Y. Liu, et al., "Projected iterative soft-thresholding algorithm for tight frames in compressed sensing magnetic resonance imaging," IEEE Transaction on Medical Imaging, vol. 35, no. 9, pp. 2130–2140, 2016.
[7] S.T. Ting, et al., "Fast implementation for compressive recovery of highly accelerated cardiac cine MRI using the balanced sparse model," Magnetic Resonance in Medicine, vol. 77, no. 4, pp. 1505–1515, 2017.
[8] Y. Hu, et al., "Spatiotemporal flexible sparse reconstruction for rapid dynamic contrast-enhanced MRI," IEEE Transactions on Biomedical Engineering, doi: 10.1109/TBME.2021.3091881, 2021.