One-dimensional Deep Low-rank and Sparse Network for Accelerated MRI(中文,English)
Zi Wang1, Chen Qian1, Di Guo2, Hongwei Sun3, Rushuai Li4, Bo Zhao5, Xiaobo Qu1,*
1the Department of Electronic Science, Fujian Provincial Key Laboratory of
Plasma and Magnetic Resonance, National Institute for Data Science in Health and Medicine, Xiamen University, Xiamen, China.
2 the School of Computer and Information Engineering, Xiamen University of Technology, Xiamen, China.
3 the United Imaging Research Institute of Intelligent Imaging, Beijing, China.
4 the Department of Nuclear Medicine, Nanjing First Hospital, Nanjing Medical University, Nanjing, China.
5 the Department of Biomedical Engineering, Oden Institute for Computational Engineering and Sciences, University of Texas at Austin, Austin, USA.
* Emails: quxiaobo <at> xmu.edu.cn or quxiaobo2009 <at> gmail.com
Citation
Zi Wang, Chen Qian, Di Guo, Hongwei Sun, Rushuai Li, Bo Zhao, Xiaobo Qu, One-dimensional Deep Low-rank and Sparse Network for Accelerated MRI, IEEE Transactions on Medical Imaging, DOI: 10.1109/TMI.2022.3203312, 2022.
Synopsis
Deep learning has shown astonishing performance in accelerated magnetic resonance imaging (MRI). Most state-of-the-art deep learning reconstructions adopt the powerful convolutional neural network and perform 2D convolution since many magnetic resonance images or their corresponding k-space are in 2D. In this work, we present a new approach that explores the 1D convolution, making the deep network much easier to be trained and generalized. We further integrate the 1D convolution into the proposed deep network, named as One-dimensional Deep Low-rank and Sparse network (ODLS), which unrolls the iteration procedure of a low-rank and sparse reconstruction model. Extensive results on in vivo knee and brain datasets demonstrate that, the proposed ODLS is very suitable for the case of limited training subjects and provides improved reconstruction performance than state-of-the-art methods both visually and quantitatively. Additionally, ODLS also shows nice robustness to different undersampling scenarios and some mismatches between the training and test data. In summary, our work demonstrates that the 1D deep learning scheme is memory-efficient and robust in fast MRI.
Main Context
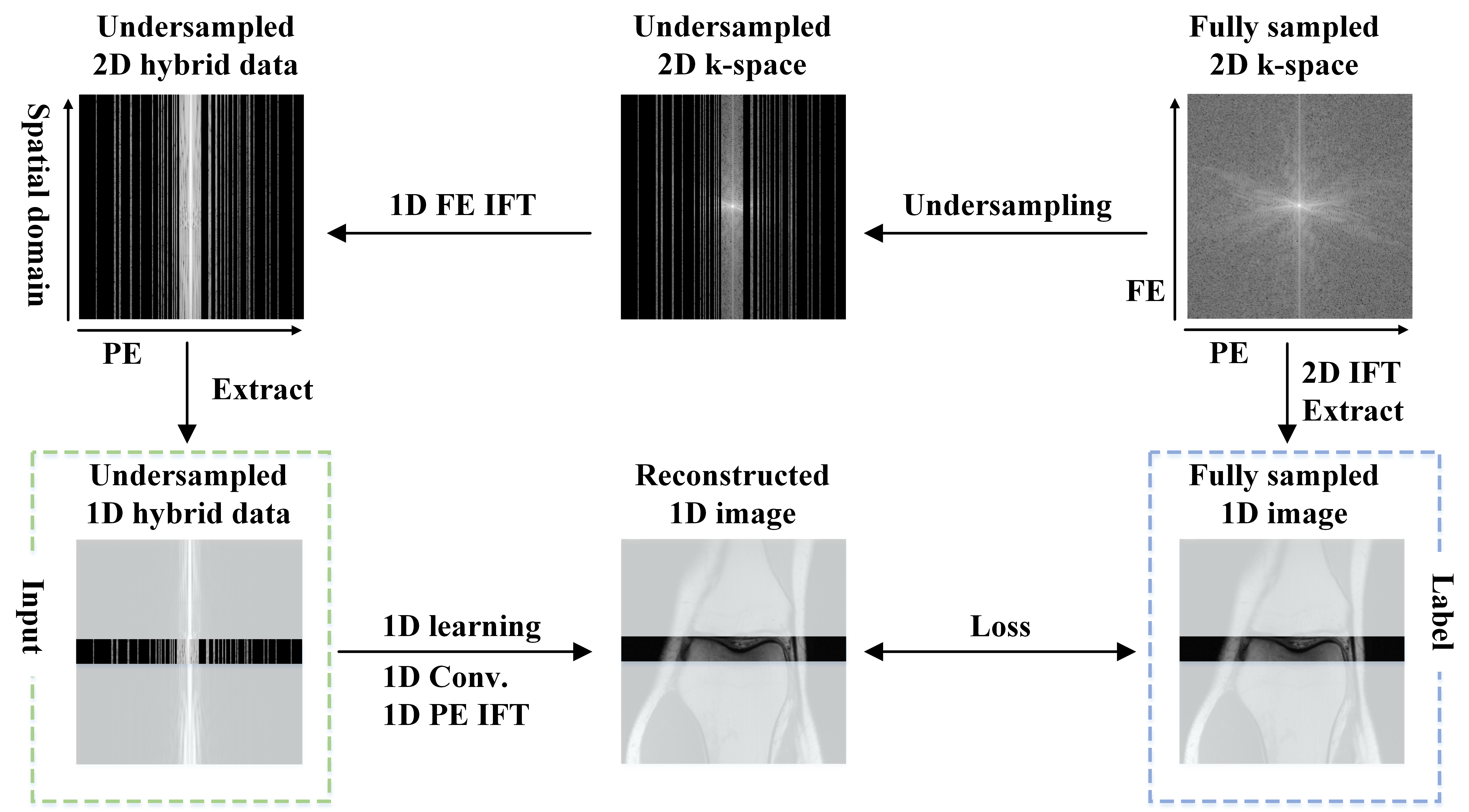
In this work, we propose a new 1D learning scheme (Fig. 1) and a One-dimensional Deep Low-rank and Sparse network (ODLS), as a high-quality, robust, memory-efficient, and fast technique for accelerated MRI, and demonstrate its benefits over other deep learning strategies. It separates the reconstruction problem along the frequency-encoded direction and leverages the resulting lower-dimensional problem structure to more easily train an unrolled network. The simple 1D convolution structure also gives us more possibilities to design more powerful network architectures without the burden of huge parameters and memory. Not limited to the 1D undersampling, we show how this mechanism can be extended to the 2D undersampling with some modifications.
Overall, the success of 1D learning in fast magnetic resonance imaging is expected to be useful for clinical applications, which only provide relatively small number of training subjects and limited computer memory.

Fig. 1. The flowchart of 1D learning. Note: The regions marked by the green and blue rectangle represent the network input and label, respectively. “Conv.” means the convolution layer. The coil dimension is omitted.
To validate the advantages of 1D learning with limited training subjects, the comparison with other state-of-the-art 2D learning networks is carried out. Figs. 2(a)-(c) show that, for any number of training subjects NTS, the proposed 1D learning ODLS consistently outperforms other 2D learning networks in terms of RLNE, PSNR, and SSIM. We can observe that ODLS can already provide better reconstructions than the baseline GRAPPA in terms of RLNE and SSIM when training subjects are very limited (NTS=2). Differently, 2D learning IUNET, DOTA, and HDSLR start to outperform the baseline GRAPPA when NTS≥4. This is because the 2D learning methods always needs a large number of training subjects to make the network sufficiently trained. The similar phenomena can also be found in the reconstruction of a brain dataset (Figs. 2(d)-(f)). These results imply that, when available training subjects are limited, the proposed method is more efficient and can provide high-quality reconstructions.
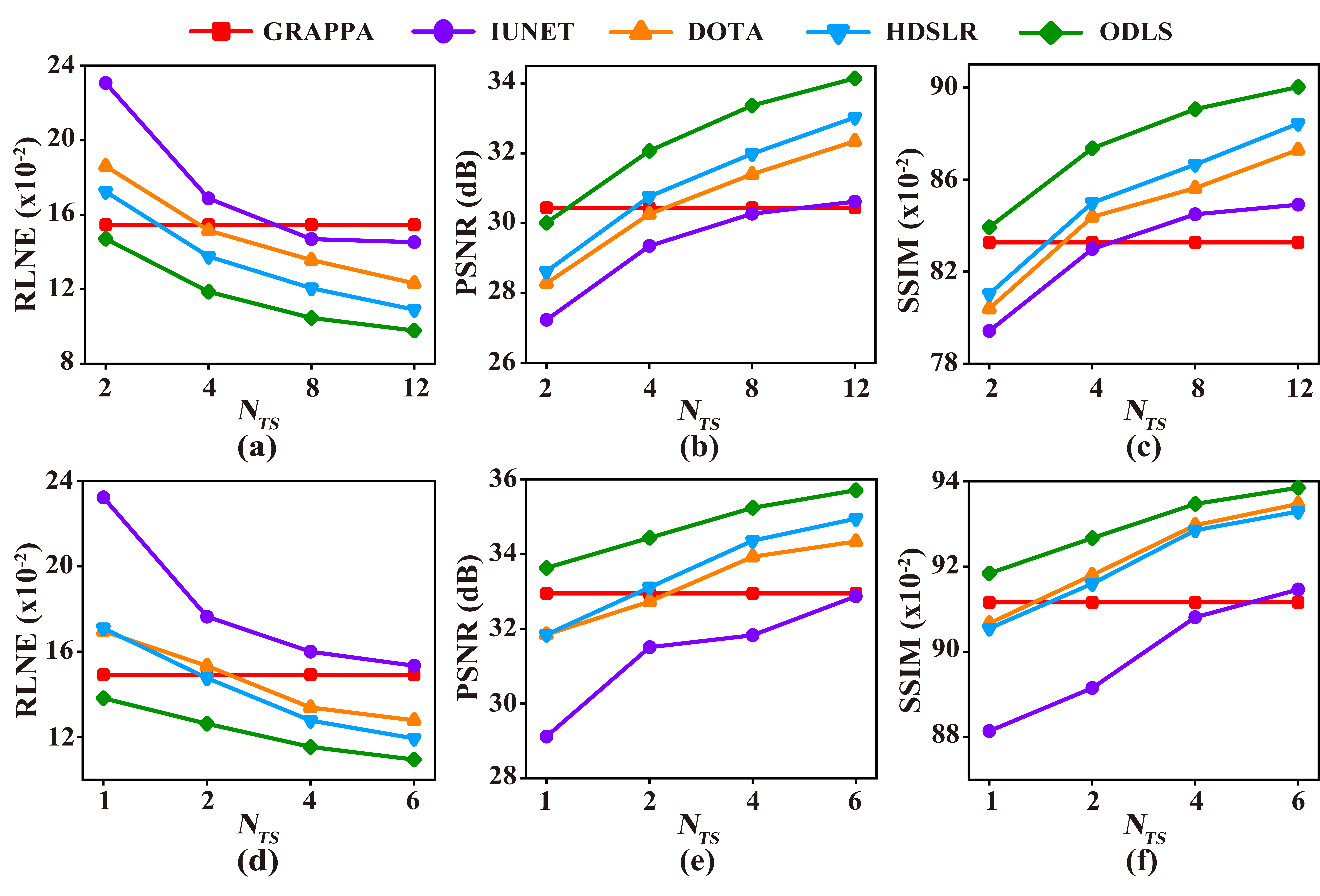
Fig. 2. Quantitative comparison of reconstructions using different number of training subjects NTS of a knee and a brain dataset. (a)-(c) are the mean of RLNE, PSNR, SSIM of the reconstructions of the coronal proton density weighted knee dataset, respectively. (d)-(f) are the mean of RLNE, PSNR, SSIM of the reconstructions of the axial T2 weighted brain dataset, respectively. Note: The Cartesian undersampling pattern with AF=4 is used. The means are computed over all test data.
A key factor that limits wide usage of existing DL for accelerated MRI is the lack of robustness. They cannot overcome the mismatch between training and test data in practical applications. It means that researchers need to spend numerous times on re-training networks to handle various reconstruction tasks, which is obviously unacceptable. Here, we focus on the three common mismatches of the knee plane orientation, brain contrast weighting, and anatomy. For the mismatch of the knee plane orientation, the networks trained by the coronal dataset were used to reconstruct the unseen sagittal one. Figs. 3(a)-(i) show that, the proposed ODLS yields the nice artifacts suppression, while other state-of-the-art methods provide the images with obvious artifacts or noises. For the mismatch of the brain contrast weighting, we trained networks by the T2 dataset to reconstruct the unseen T1 one. The results in Figs. 3(j)-(r) show that, ODLS provides better reconstructions than other methods visually. For the mismatch of the anatomies, i.e., the networks trained by the coronal knee dataset were used to reconstruct the unseen T1 brain. The results in Figs. 3(s)-(v) show that, ODLS still provides best reconstructions among all deep learning methods, GRAPPA, JSENSE, and SAKE visually. These results demonstrate that, the proposed ODLS has significantly improved generalization capabilities than compared deep learning methods, and can also provide better details preservation than compared untrained methods.
More excellent performance of ODLS in different undersampling patterns and mismatched scenarios, and the extension of high-dimensional MRI reconstruction can be found in the full-length paper.
Fig. 3. Mismatched reconstructions under the Cartesian undersampling patterns with AF=4. (a) (or (j)) is the fully sampled image. (b)-(e) (or (k)-(n)) are reconstructed images from untrained methods. (f)-(i), (o)-(r), and (s)-(v) are reconstructed images from deep learning methods in three mismatch scenarios.
Shared Materials
Acknowledgements
This work was supported in part by the National Natural Science Foundation of China under grants 62122064, 61971361, and 61871341, the Natural Science Foundation of Fujian Province of China under grant 2021J011184, President Fund of Xiamen University under grant 0621ZK1035, and the Xiamen University Nanqiang Outstanding Talents Program.
References
[1] M. Lustig, D. Donoho, and J. M. Pauly, “Sparse MRI: The application of compressed sensing for rapid MR imaging,” Magn. Reson. Med., vol. 58, no. 6, pp. 1182-1195, 2007.
[2] K. P. Pruessmann, M. Weiger, M. B. Scheidegger, and P. Boesiger, “SENSE: Sensitivity encoding for fast MRI,” Magn. Reson. Med., vol. 42, no. 5, pp. 952-962, 1999.
[3] M. A. Griswold et al., “Generalized autocalibrating partially parallel acquisitions (GRAPPA),” Magn. Reson. Med., vol. 47, no. 6, pp. 1202-1210, 2002.
[4] Z. Liang, “Spatiotemporal imaging with partially separable functions,” in 4th IEEE International Symposium on Biomedical Imaging (ISBI), 2007, pp. 988-991.
[5] Y. Yang, F. Liu, Z. Jin, and S. Crozier, “Aliasing artefact suppression in compressed sensing MRI for random phase-encode undersampling,” IEEE Trans. Biomed. Eng., vol. 62, no. 9, pp. 2215-2223, 2015.
[6] X. Zhang et al., “A guaranteed convergence analysis for the projected fast iterative soft-thresholding algorithm in parallel MRI,” Med. Image Anal., vol. 69, 101987, 2021.
[7] X. Zhang et al., “Accelerated MRI reconstruction with separable and enhanced low-rank Hankel regularization,” IEEE Trans. Med. Imaging, DOI: 10.1109/TMI.2022.3164472, 2022.
[8] P. J. Shin et al., “Calibrationless parallel imaging reconstruction based on structured low-rank matrix completion,” Magn. Reson. Med., vol. 72, no. 4, pp. 959-970, 2014.
[9] J. P. Haldar and J. Zhuo, “P-LORAKS: Low-rank modeling of local k-space neighborhoods with parallel imaging data,” Magn. Reson. Med., vol. 75, no. 4, pp. 1499-1514, 2016.
[10] J. C. Ye, Y. Han, and E. Cha, “Deep convolutional framelets: A general deep learning framework for inverse problems," SIAM J. Imaging Sci., vol. 11, no. 2, pp. 991-1048, 2018.
[11] T. Eo, H. Shin, Y. Jun, T. Kim, and D. Hwang, “Accelerating Cartesian MRI by domain-transform manifold learning in phase-encoding direction,” Med. Image Anal., vol. 63, 101689, 2020.
[12] A. Pramanik, H. Aggarwal, and M. Jacob, “Deep generalization of structured low-rank algorithms (Deep-SLR),” IEEE Trans. Med. Imaging, vol. 39, no. 12, pp. 4186-4197, 2020.
[13] K. Hammernik et al., “Learning a variational network for reconstruction of accelerated MRI data,” Magn. Reson. Med., vol. 79, no. 6, pp. 3055-3071, 2018.
[14] F. K. Zbontar et al., “FastMRI: An open dataset and benchmarks for accelerated MRI,” arXiv: 1811.08839, 2019.
[15] L. Ying and J. Sheng, “Joint image reconstruction and sensitivity estimation in SENSE (JSENSE),” Magn. Reson. Med., vol. 57, no. 6, pp. 1196-1202, 2007.
[16] Q. Yang, Z. Wang, K. Guo, C. Cai, and X. Qu, “Physics-driven synthetic data learning for biomedical magnetic resonance,” IEEE Signal Process. Mag., DOI: 10.1109/MSP.2022.3183809, 2022.
[17] Z. Wang et al., “A sparse model-inspired deep thresholding network for exponential signal reconstruction--Application in fast biological spectroscopy,” IEEE Trans. Neural Netw. Learn. Syst., DOI: 10.1109/TNNLS.2022.3144580, 2022.