Exponential Signal Reconstruction with Deep Hankel Matrix Factorization (中文,English)
Yihui Huang1, Jinkui Zhao1, Zi Wang1, Vladislav Orekhov2, Di Guo3, Xiaobo Qu1,*
1 the Department of Electronic Science, Fujian Provincial Key Laboratory of
Plasma and Magnetic Resonance, Biomedical Intelligent Cloud R&D Center, National Institute for Data Science in
Health and Medicine, Xiamen University, Xiamen, China
2 Department of Chemistry and Molecular Biology and Swedish NMR Centre, University of Gothenburg, Box
465, Gothenburg 40530, Sweden.
3 School of Computer and Information Engineering, Xiamen University of Technology, Xiamen, China
* Emails: quxiaobo <at> xmu.edu.cn or quxiaobo2009 <at> gmail.com
Citation
Yihui Huang, Jinkui Zhao, Zi Wang, Vladislav Orekhov, Di Guo, Xiaobo Qu, Exponential Signal Reconstruction With Deep Hankel Matrix Factorization, IEEE Transactions on Neural Networks and Learning Systems, doi: 10.1109/TNNLS.2021.3134717, 2022
Abstract
Exponential function is a fundamental signal form in signal processing. Representative application fields of
exponential signals include communication, imaging, electronic system and NMR spectroscopy. For fast data
acquisition or other inevitable reasons, only a small amount of samples may be acquired. How to reconstruct under
sampled exponentials is one of the fundamental problems and frontiers in signal processing. Existing iterative
algorithms, such as low rank, are time consuming, while the reconstruction error of the state-of-the-art deep
learning method, especially for the low low-intensity signals, still needs to be reduced.
In this work, we propose a deep learning neural network called Deep Hankel Matrix Factorization network (DHMF) to
recover exponentials by imitating the established model-based low-rank Hankel reconstruction algorithm. Our design
starts from constraining the low rank property of the Hankel matrix which is arranged from exponential signals and
adopts matrix factorization-based Low-Rank Hankel Matrix Completion which are SVD-free. Given the success of the
training network using solely synthetic data, we also synthesize exponentials and then feed into the network to
learn the mapping from under sampled exponentials, to fully sampled exponentials.
Compared with the state-of-the-art model-based and DL-based methods, DHMF is much faster than the former, and
possess a more understandable network architecture than the latter. DHMF also achieves lower reconstruction error
than the compared methods on both synthetic and realistic NMR data, and can preserve the low intensity signals much
better.
Method
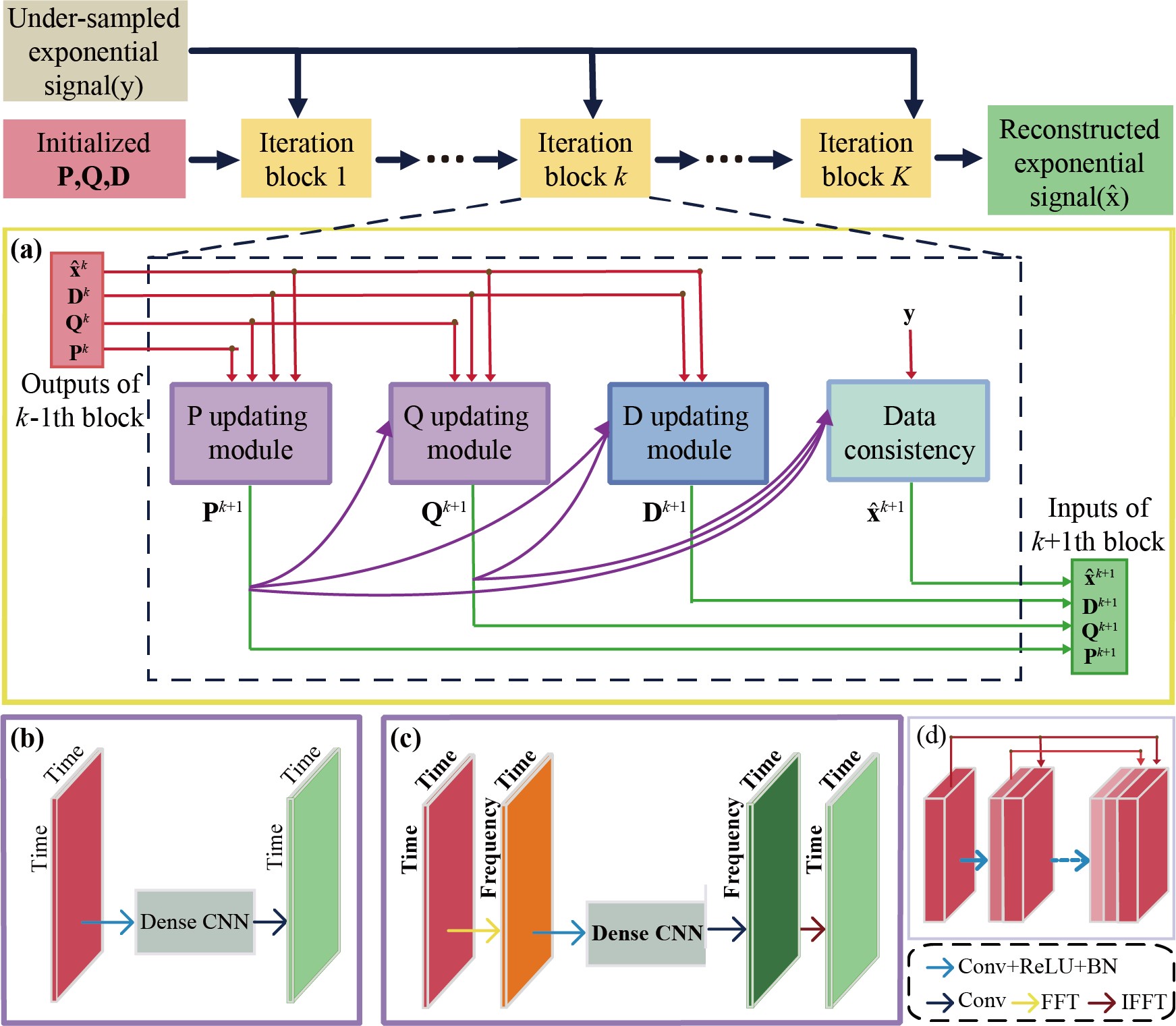
The proposed DHMF consists of three updating modules P, Q, D and one data consistency module (Fig. 1).

Fig. 1. The architecture of DHMF. (a) the general process of the k-th block, (b) P/Q modules with time domain convolution in the basic DHMF, (c) P/Q modules with frequency domain convolution in the enhanced DHMF, (d) dense convolutional neural network.
Each updating modules of $k\text{-th(}k=1,2...,K)$ block are designed as: $$\begin{align} & {{\mathbf{P}}^{k+1}}={{\mathsf{\mathcal{P}}}^{k}}((\mathsf{\mathcal{R}}{{{\mathbf{\hat{x}}}}^{k}}+{{\mathbf{D}}^{k}}){{\mathbf{Q}}^{k}},{{\mathbf{Q}}^{k}},{{\mathbf{P}}^{k}}) \\ & {{\mathbf{Q}}^{k+1}}={{\mathsf{\mathcal{Q}}}^{k}}({{(\mathsf{\mathcal{R}}{{{\mathbf{\hat{x}}}}^{k}}+{{\mathbf{D}}^{k}})}^{H}}{{\mathbf{P}}^{k+1}},{{\mathbf{P}}^{k+1}},{{\mathbf{Q}}^{k}}) \\ & {{\mathbf{D}}^{k+1}}={{\mathbf{D}}^{k}}+\tau (\mathsf{\mathcal{R}}{{{\mathbf{\hat{x}}}}^{k}}-{{\mathbf{P}}^{k+1}}{{({{\mathbf{Q}}^{k+1}})}^{H}}) \\ & {{{\mathbf{\hat{x}}}}^{k+1}}=\mathsf{\mathcal{S}}(\mathbf{y},{{\mathsf{\mathcal{R}}}^{*}}({{\mathbf{P}}^{k+1}}{{({{\mathbf{Q}}^{k+1}})}^{H}}-{{\mathbf{D}}^{k+1}})) \\ \end{align}$$ where $\mathsf{\mathcal{P}}$ and $\mathsf{\mathcal{Q}}$ are updating operators, $\mathsf{\mathcal{S}}$denotes the data consistency operator, $\tau $is the learning step, $\mathsf{\mathcal{R}}$denotes the Hankel operator mapping the vector to a Hankel matrix while ${{\mathsf{\mathcal{R}}}^{*}}$ is the corresponding inverse operator. The final loss function is $$\mathsf{\mathcal{L}}(\Theta )=\frac{1}{Q}\sum\limits_{q=1}^{Q}{\sum\limits_{k=1}^{K}{(||\mathbf{\hat{x}}_{q}^{k}({{\Theta }^{{}}})-{{\mathbf{x}}_{q}}||_{2}^{2}}}+\gamma ||{{\mathsf{\mathcal{R}}}^{*}}(\mathbf{P}_{q}^{k}(\Theta )\mathbf{Q}_{q}^{k}(\Theta )_{{}}^{H})-{{\mathbf{x}}_{q}}||_{2}^{2})$$, where $\gamma $ is the regularization parameter. Subscript q means the q-th index in training data of the total Q sampling trail. $\Theta $ is the learnable network parameters including all the learnable weights of convolution layers and batch normalization layers in P and Q updating module.
Main Results
We evaluate the performance of the proposed DHMF on both synthetic exponential signals and realistic biological NMR spectroscopy with three state-of-the-art approaches, including LRHM [8], LRHMF [10], and DLNMR [14]. Both LRHM and LRHMF are typical model-based iterative algorithms,DLNMR is a state-of-the-art deep learning method for exponential signal reconstruction.
1. Network Interpretation
Fig.2 imply that DHMF implicitly learns the approximation of low rank property, and can provide a better interpretation of the reconstruction in the network.
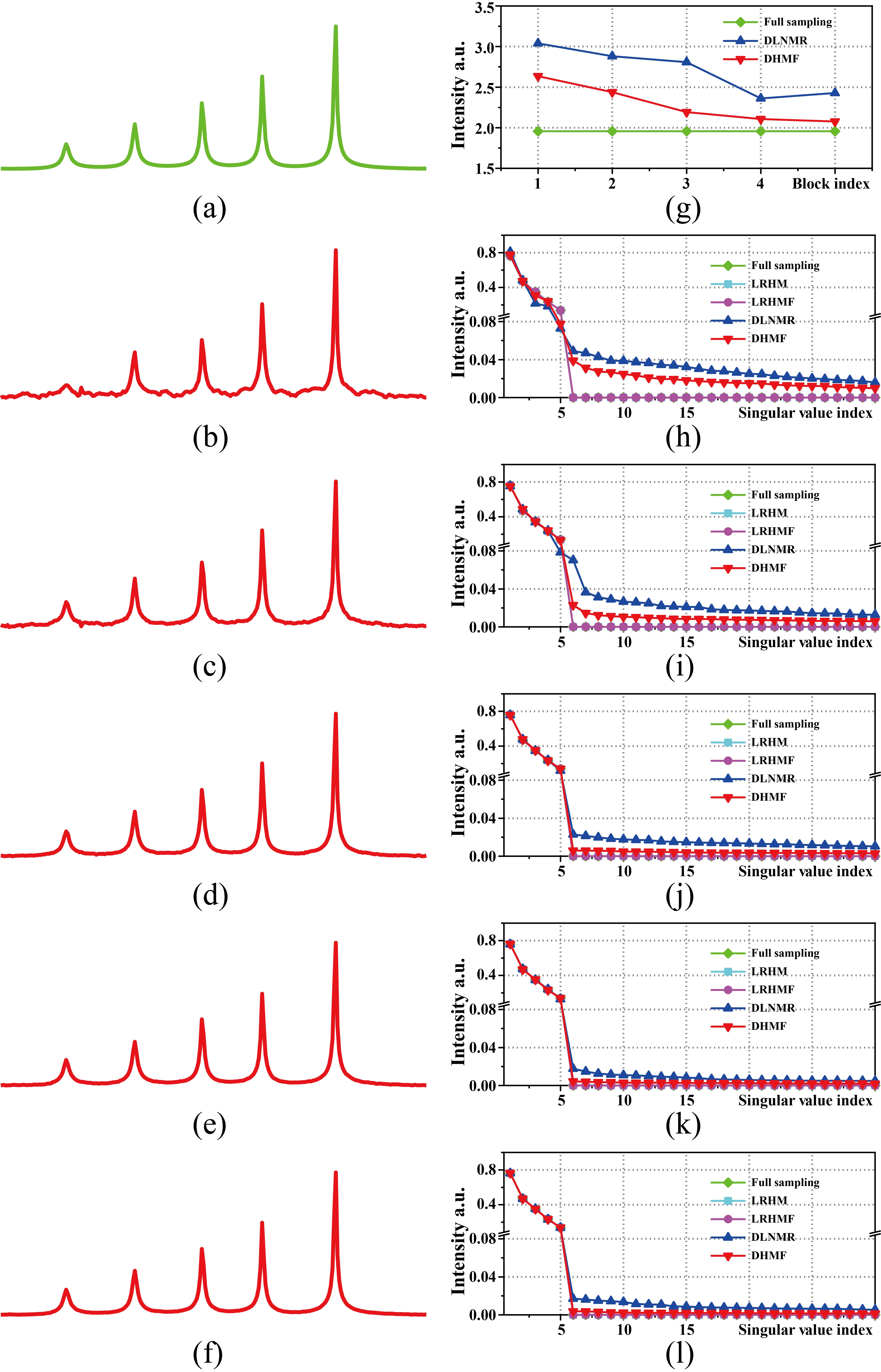
Fig. 2. The reconstructed spectra and singular values at each block. (a) fully sampled spectrum, (b)-(f) the reconstructed spectrum by the 1st to 5th blocks, (g) the nuclear norm of Hankel matrix of time domain signal, and (h)-(l) denote corresponding singular values of the ouput of each block.
2. Reconstruction of Synthetic Data
Fig.3 shows that DHMF can reconstruct signals that have a larger number of exponentials or with fewer samples. Fig.4 shows that DHMF provides the most consistent spectral peak shape and intensity, and significantly possesses the highest correlation on the weakest peak and better performance on another low-intensity peak.
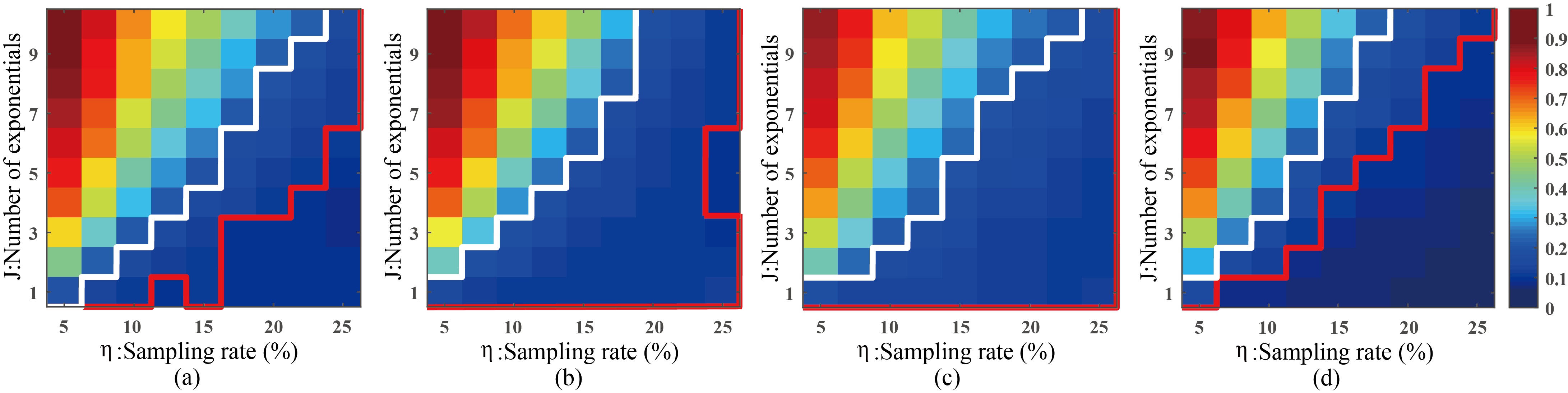
Fig. 3. Average reconstruction error, RLNE, for the synthetic signal. (a) LRHM, (b)LRHMF, (c) DLNMR, (d)DHMF. Note: Each color reflects the average RLNEs over 100 Monte Carlo trials of undersamplings. Red (or white) line indicates an empirical boundary where the threshold of reconstruction error, RLNE, is 0.1 (or 0.2). The reconstruction error in the upper region above (or lower region below) the boundary is greater (or lower) than the threshold. The DLNMR did not obtain any smaller reconstruction error than 0.1 thus the region below the red line is empty.
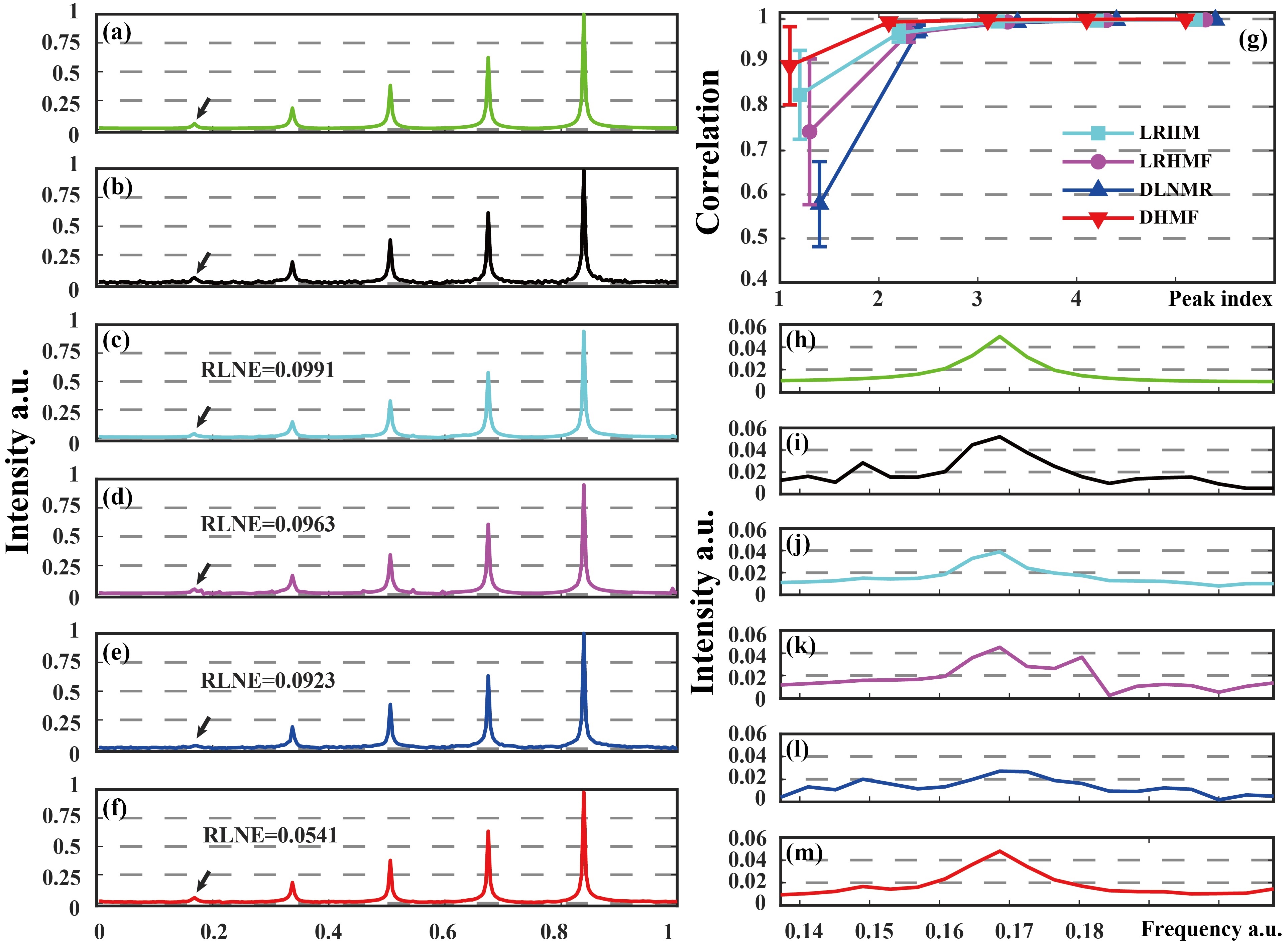
Fig. 4. Reconstructed synthetic signals with low-intensity peaks. (a) is the fully sampled noise-free signal, (b) is the noisy data with the additive Gaussian noise under standard deviation of 0.05, (c-f) are reconstructions obtained by LRHM, LRHMF, DLNMR, and DHMF from 25% data, respectively, (h-m) are the zoomed in weakest peaks marked by the arrow. (g) is the Pearsons linear correlation coefficient of each peak.
3. Reconstruction of Realistic NMR Data
Experiments on one 1H-15N TROSY spectrum (Fig. 5(a)) and one 1H-15N HSQC spectrum (Fig. 6(a)) show that DHMF provides the most faithful reconstruction for the realistic NMR spectra.
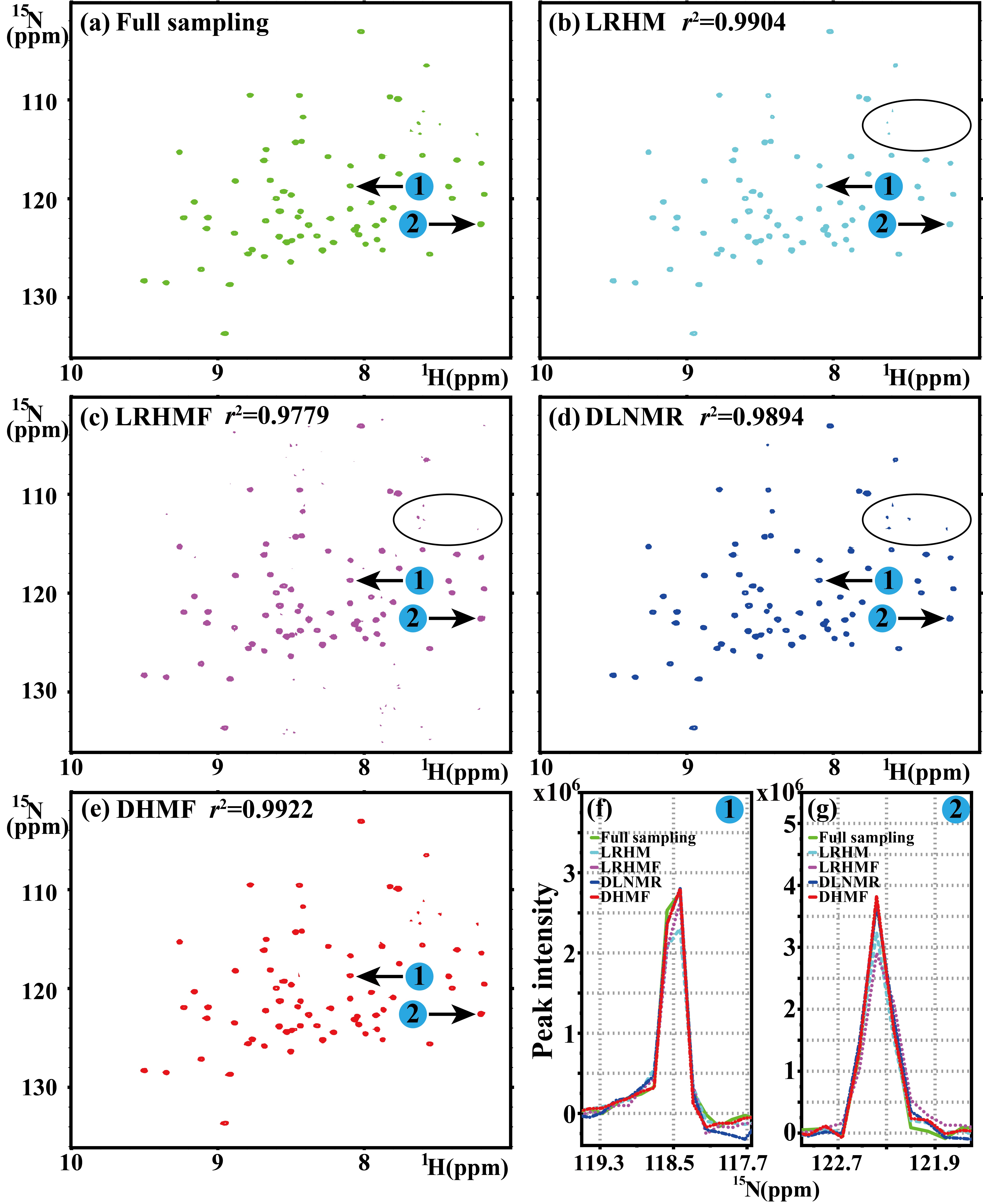
Fig. 5. The reconstruction of 2D 1H-15N TROSY spectrum of Ubiquitin. (a) is the fully sampled NMR spectrum, (b)-(e) are the reconstructions by LRHM, LRHMF, DLNMR, and DHMF, respectively. The ppm denotes parts per million by frequency, which is the unit of chemical shift.. (f) and (g) are zoomed out 1D 15N traces. Note: The data size is 127×512 and undersampling is performed on the dimension of 127 at sampling rate 25%. Note: The peak intensity correlations r2 are added in the corresponding spectra.
Fig. 6. The reconstruction of 2D 1H-15N HSQC spectrum of protain. (a) is the fully sampled NMR spectrum, (b)-(e) are the reconstructions by LRHM, LRHMF, DLNMR, and DHMF, respectively. (f) and (g) are zoomed out 1D 15N traces. Note: The data size is 255×116 and the undersampling is performed on the dimension of 255 at sampling rate 25%. Note: The peak intensity correlations r2 are added in the corresponding spectra.
Download
Acknowledgments
1) Data and hardware Provider
The authors would like to thank Vladislav Orekhov and Maxim Mayzel for sharing the NMR data and the GPU donated by NVIDIA Corporation. The authors thank the China Mobile Group for providing e-Cloud service. The authors thank China Mobile Group for providing e-Cloud service.
2) Fund
This work was supported in part by the National Natural Science Foundation of China (62122064, 61971361, 61871341, and 61811530021), the National Key R&D Program of China (2017YFC0108703), and Xiamen University Nanqiang Outstanding Talents Program.
References
[1] A. Hirose and S. Yoshida, "Generalization characteristics of complexvalued feedforward neural networks in
relation to signal coherence," IEEE Trans. Neural Netw. Learn. Syst., vol. 23, no. 4, pp. 541-551, 2012.
[2] C. Qian, L. Huang, M. Cao, J. Xie, and H. C. So, "PUMA: An improved realization of MODE for DOA estimation,"
IEEE Trans. Aerosp. Electron. Syst., vol. 53, no. 5, pp. 2128-2139, 2017.
[3] D. Nion and N. D. Sidiropoulos, "Tensor algebra and multidimensional harmonic retrieval in signal processing for
mimo radar," IEEE Trans. Signal Process., vol. 58, no. 11, pp. 5693-5705, 2010.
[4] L. Schermelleh, R. Heintzmann, and H. Leonhardt, "A guide to superresolution fluorescence microscopy," J. Cell
Biol., vol. 190, no. 2, pp. 165-175, 2010.
[5] J. A. Tropp, J. N. Laska, M. F. Duarte, J. K. Romberg, and R. G. Baraniuk, "Beyond Nyquist: Efficient sampling
of sparse bandlimited signals," IEEE Trans. Inf. Theory, vol. 56, no. 1, pp. 520-544, 2010.
[6] M. Vetterli, P. Marziliano, and T. Blu, "Sampling signals with finite rate of innovation," IEEE Trans. Signal
Process., vol. 50, no. 6, pp. 1417-1428, 2002.
[7] M. Elad, P. Milanfar, and G. Golub, H, "Shape from moments – an estimation theory perspective," IEEE Trans.
Signal Process., vol. 52, no. 7, pp. 1814-1829, 2004.
[8] X. Qu, M. Mayzel, J.-F. Cai, Z. Chen, and V. Orekhov, "Accelerated NMR spectroscopy with low-rank
reconstruction," Angew. Chem.-Int. Edit., vol.54, no. 3, pp. 852-854, 2015.
[9] H. M. Nguyen, X. Peng, M. N. Do, and Z.-P. Liang, "Denoising MR spectroscopic imaging data with low-rank
approximations," IEEE Trans. Biomed. Eng., vol. 60, no. 1, pp. 78-89, 2013.
[10] D. Guo, H. Lu, and X. Qu, "A fast low rank Hankel matrix factorization reconstruction method for non-uniformly
sampled magnetic resonance spectroscopy," IEEE Access, vol. 5, pp. 16033-16039, 2017.