Image Reconstruction with Low-rankness and Self-consistency of k-space Data in Parallel MRI (中文,English)
Xinlin Zhang1, Di Guo2, Yiman Huang1, Ying Chen1, Liansheng Wang3, Feng Huang4, Qin Xu4, Xiaobo Qu1,*
1 Department of Electronic Science, Fujian Provincial Key Laboratory of Plasma and Magnetic Resonance, School of Electronic Science and Engineering, National Model Microelectronics College, Xiamen University, Xiamen 361005, China.
2 Schoolof Computer and Information Engineering, Fujian Provincial University Key Laboratory of Internet of Things Application Technology, Xiamen University of Technology, Xiamen 361024, China.
3 Department of Computer Science, School of Information Science and Engineering, Xiamen University, Xiamen 361005, China.
4 Neusoft Medical System, Shanghai 200241, China.
* Emails: quxiaobo <at> xmu.edu.cn or quxiaobo2009 <at> gmail.com
Citation
Xinlin Zhang, Di Guo, Yiman Huang, Ying Chen, Liansheng Wang, Feng Huang, Qin Xu, Xiaobo Qu, Image Reconstruction with Low-rankness and Self-consistency of k-space Data in Parallel MRI, Medical Image Analysis, 63: 101687, 2020.
Synopsis
Parallel magnetic resonance imaging has served as an effective and widely adopted technique for accelerating data collection. The advent of sparse sampling offers aggressive acceleration, allowing flexible sampling and better reconstruction. Nevertheless, faithfully reconstructing the image from limited data still poses a challenging task. Recent low-rank reconstruction methods are superior in providing high-quality images. Nevertheless, none of them employ the routinely acquired calibration data to improve image quality in parallel magnetic resonance imaging.
In this work, an image reconstruction approach named STDLR-SPIRiT is proposed to explore the simultaneous two-directional low-rankness (STDLR) in the k-space data and to mine the data correlation from multiple receiver coils with the iterative self-consistent parallel imaging reconstruction (SPIRiT). Experimental results of phantom and brain imaging data show that the proposed method outperforms the state-of-the-art methods in terms of suppressing artifacts and achieving the lowest error. Moreover, the proposed method exhibits robust reconstruction even when the auto-calibration signals are limited in parallel imaging. Overall the proposed method can be exploited to achieve better image quality for accelerated parallel magnetic resonance imaging.
Method
1. Background
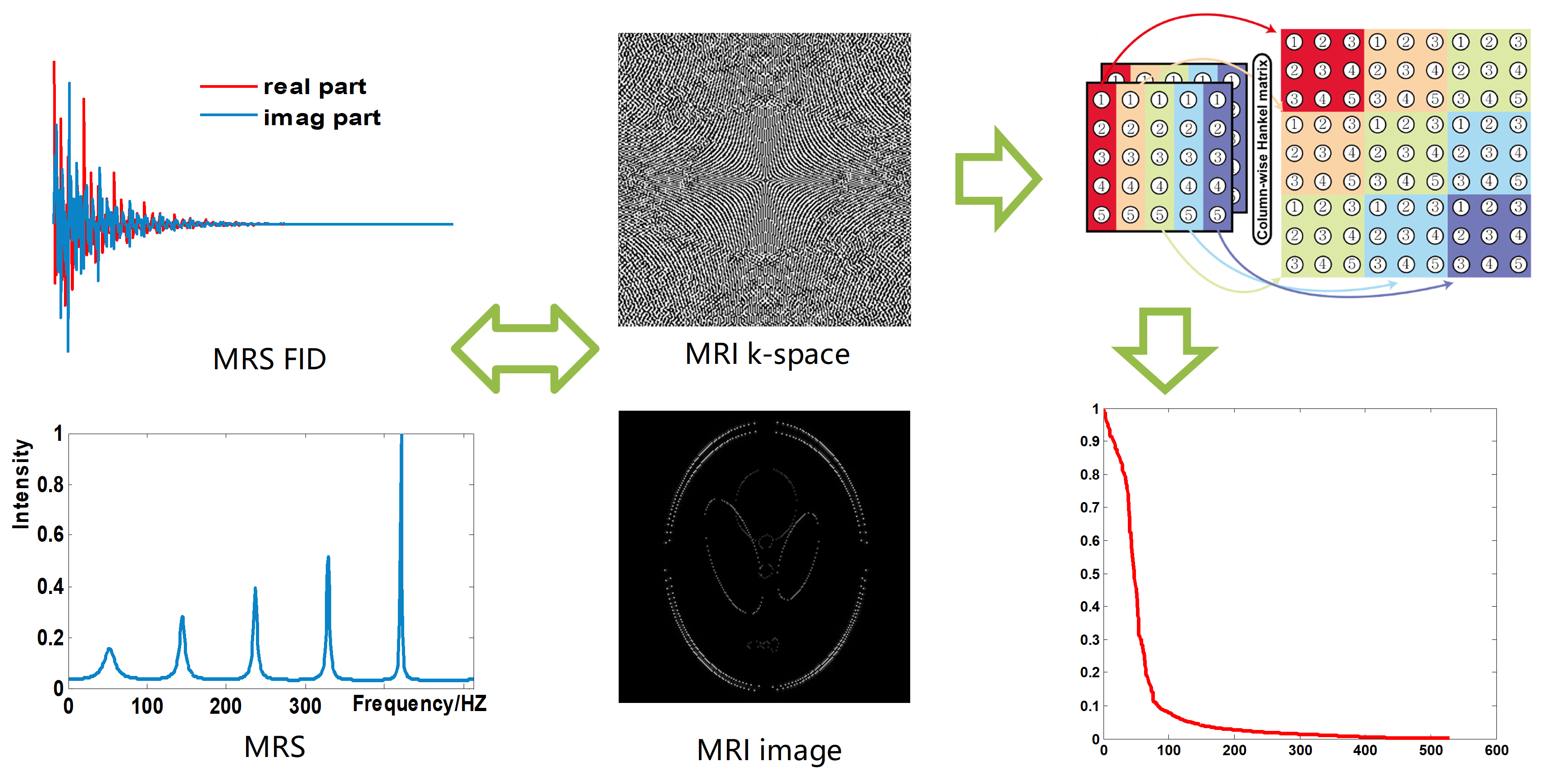
Prolonged acquisition time poses a challenging task in magnetic resonance imaging (MRI). Parallel imaging technology significantly reduces the scan time, however, limited by the requirement of sufficient auto-calibration signal (ACS). Sparse sampling with reconstruction is another effective way to speed up the data acquisition duration, and the reconstruction methods that could be categorized into two main classes: sparsity approach and low-rankness approaches. Rooting from low rankness methods, the recent emergence of low-rank structured matric methods, was first used in magnetic resonance spectroscopy (MRS) reconstruction. In this type of methods, the free induction decay signal (FID) of MRS in time domain is modeled as the sum of exponential functions, and the reconstruction is carried out by constraining the low rankness of Hankel matrix composed of FID, and exhibit promising reconstruction results.
Recently, the exponential function property of MRS is gradually extended to MRI, that is, k-space in MRI is modeled as the sum of exponential functions, and reconstruct MRI image by imposing low rank constraint on the structured matrix composed of k-space (Fig. 1). However, there are still limitations of the methods, for instance, separately enforcing the low rankness of horizontal and vertical directions results in suboptimal solution in ALOHA, existed low-rank structured matric methods did not take advantage of the common acquired ACS to help improve reconstruction performance. Here we proposed a k-space domain reconstruction method that concurrently explores the low-rankness of k-space data and calibration data. The low rankness was exploited by minimizing the low-rankness of the two-directional weighting of the k-space. In addition, intra- and inter-coil data relationships are enforced in the form of self-consistency over k-space.

Fig. 1. Low rankness of structured matrix in MRS an MRI.
2. Simultaneous two-directional low-rankness and iterative self-consistent parallel imaging reconstruction (STDLR-SPIRiT)
It has been proved that the sparsity of image has a close relationship to the low rankness of the k-space data (Fig. 2). The recovery of missing k-space data can be done through minimizing a matrix completion problem with the enforcement of low rankness of the Hankel matric of weighting k-space data. We proposed a reconstruction method named STDLR-SPIRiT to exploit the simultaneous two-directional low rankness of k-space data and the information of ACS signal utilized with a SPIRiT term:
$$ \left( \mathbf{STDLR-SPIRiT}\right)\quad \underset{\mathbf{X}}{\mathop{\min }}\,\sum\limits_{i}{{{\left\| \tilde{\mathcal{H}}{{\mathcal{W}}_{i}}\mathbf{X} \right\|}_{*}}}+\frac{{{\lambda }_{1}}}{2}\left\| \mathcal{G}\mathbf{X}-\mathbf{X} \right\|_{F}^{2}+\frac{{{\lambda }_{2}}}{2}\left\| \mathbf{Y}-\mathcal{U}\mathbf{X} \right\|_{F}^{2}, $$ where $i$ denotes $=$ or $\bot $, i.e. horizontal and vertical directions. $\mathbf{X}=\left[ {{\mathbf{X}}_{1}},{{\mathbf{X}}_{2}},\cdots ,{{\mathbf{X}}_{J}} \right]$ denotes the targeted k-space data from all coils and $\mathbf{Y}=\left[ {{\mathbf{Y}}_{1}},{{\mathbf{Y}}_{2}},\cdots ,{{\mathbf{Y}}_{J}} \right]$ the acquired k-space data with zero-filling at non-acquired positions, $\mathcal{U}$ the operator that performs undersampling and zerofilling on non-acquired data points. $\tilde{\mathcal{H}}{{\mathcal{W}}_{i}}\mathbf{X}=\left[ \mathcal{H}{{\mathbf{W}}_{i}}\odot {{\mathbf{X}}_{1}},\cdots ,\mathcal{H}{{\mathbf{W}}_{i}}\odot {{\mathbf{X}}_{J}} \right]$, where $\mathcal{H}$ is an operator that converts a matrix into a block Hankel matrix and ${{\mathbf{W}}_{i}}$ denote the weights which are the Fourier transform of filters in the horizontal or vertical directions, $\mathcal{G}$ is an operator that convolves the k-space data with a series of calibration kernels that are estimated from ACS. ${{\left\| \cdot \right\|}_{*}}$ imposes the low-rank constraint on the weighted Hankel structured matrix, ${{\lambda }_{1}}$ and ${{\lambda }_{2}}$ trade off among the low-rank constraint, self-calibration consistency and undersampled data fidelity. The schematic illustration of STDLR-SPIRiT is depicted in Fig. 3.
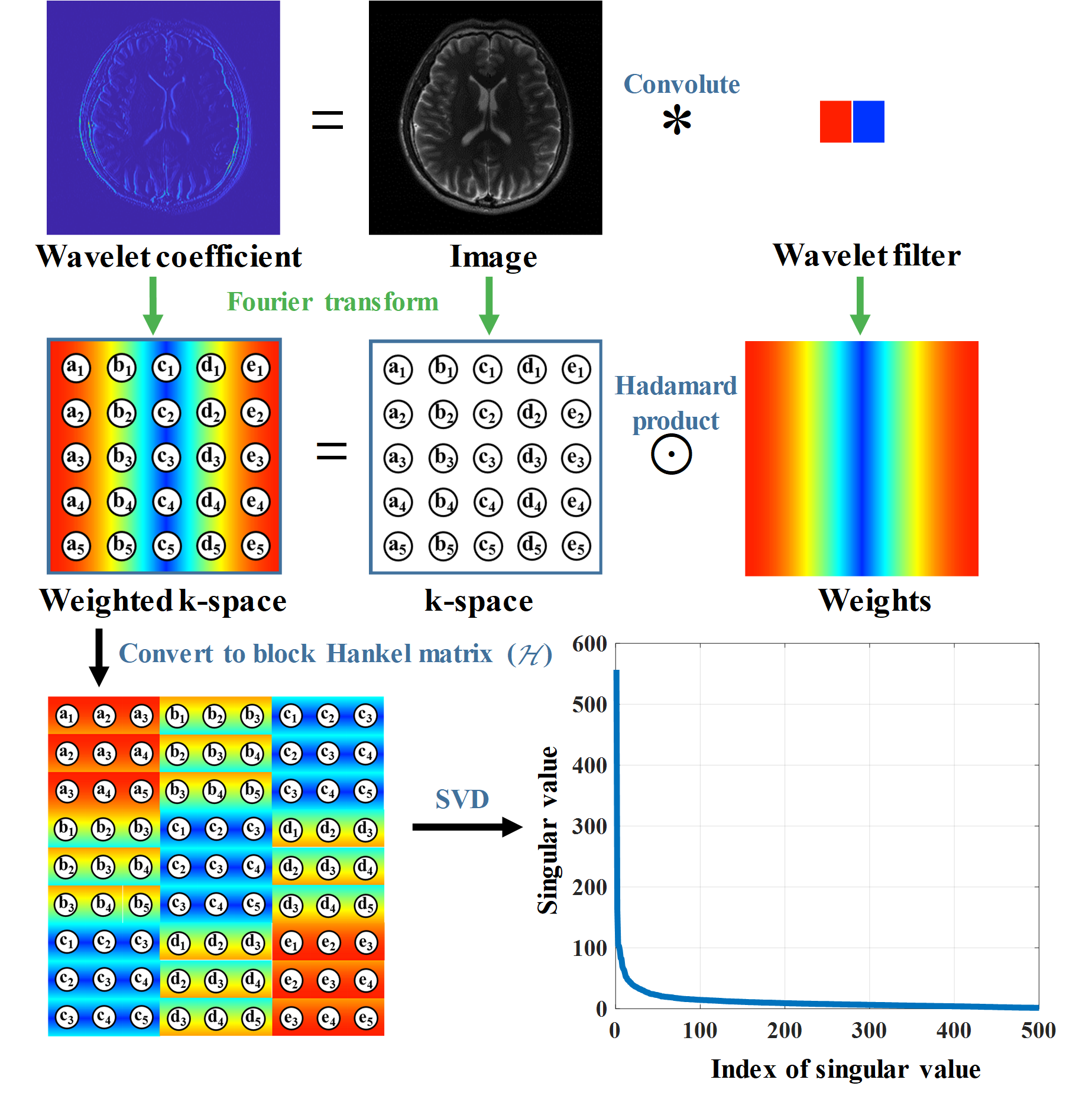
Fig. 2. The illustration of low-rankness of weighted k-space with wavelet filters.

Fig. 3. The flow chart of the proposed method.
3. Main result
The proposed method, STDLR-SPIRiT, is compared with three state-of-the-art reconstruction methods including GRAPPA, $\ell_1$-SPIRiT and ALOHA. A 4-coil in vivo human brain MRI data was adopted in experiments, and the acceleration factor R=3. We adopt relative L2 norm error (RLNE) as objective criteria to quantify the reconstruction performance. A lower RLNE demonstrates higher consistency between the fully sampled image and the reconstructed image.
As shown in Fig. 4, GRAPPA (Fig. 4 (b)) and ALOHA (Fig. 4 (d)) produce image with obvious artifacts while $\ell_1$-SPIRiT (Fig. 4 (c)) and STDLR-SPIRiT (Fig. 4 (e)) provide much better reconstructed image with good artifacts suppression. But, when inspecting on zoom-in images, we can find relatively stronger noise and somewhat blur of details in the $\ell_1$-SPIRiT reconstruct image. The proposed STDLR-SPIRiT reconstructs an image with better signal to noise ratio and fine details preservation. Moreover, as shown in Fig. 5, STDLR-SPIRiT shows robustness to the number of ACS lines.
Fig.4. Reconstruction results and errors of 4-coil human brain data using the Cartesian pattern with a sampling rate of 0.34. (a) An SSOS image of fully sampled data; (b-e) SSOS images of reconstructed results by GRAPPA, $\ell_1$-SPIRiT, ALOHA and STDLR-SPIRiT, respectively; (f) the Cartesian undersampling pattern; (g-j) the reconstruction error distribution corresponding to reconstructed image above them. Note: the RLNEs of (b-e) are 0.1335, 0.0866, 0.1117, 0.0735, respectively.
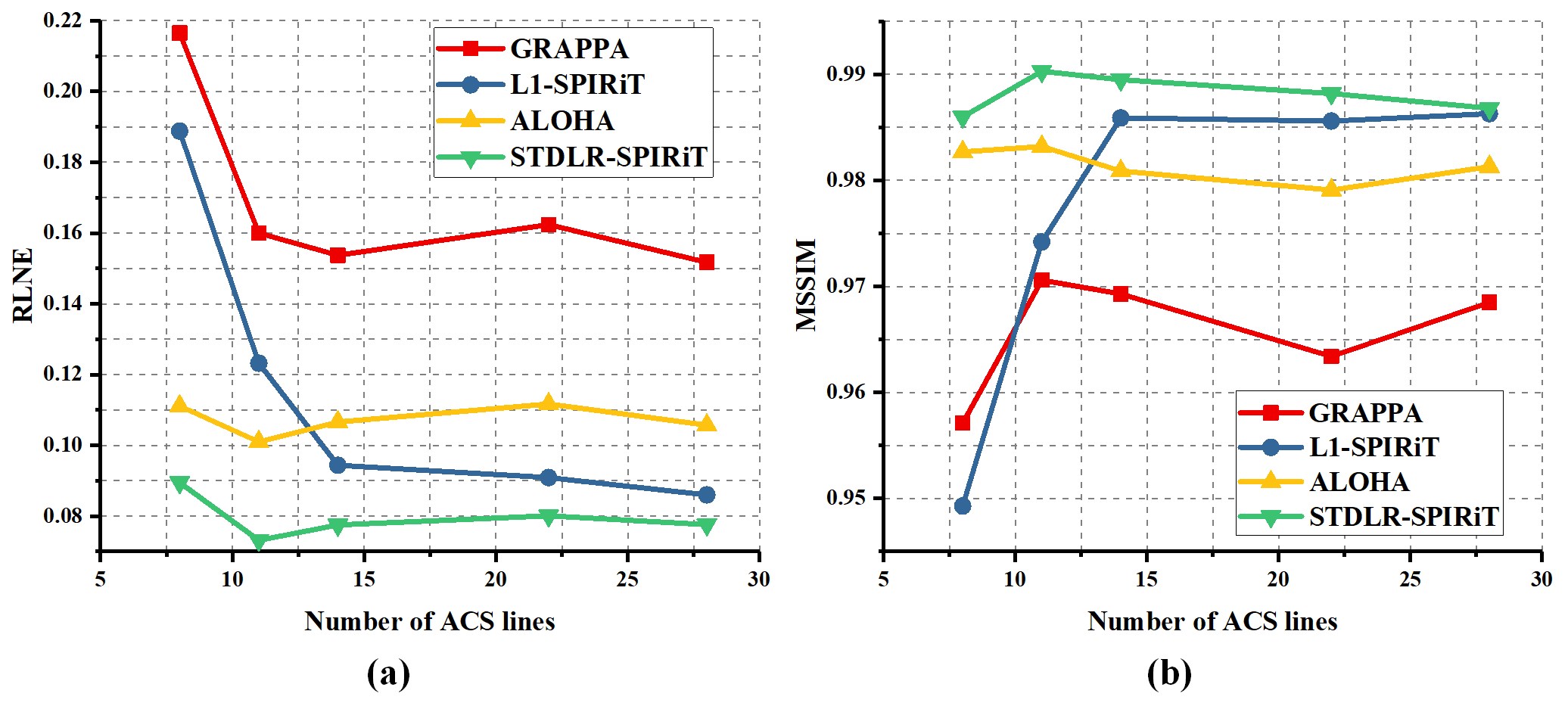
Fig.5. The variation trends of RLNE (a) and MSSIM (b) versus the number of ACS lines. This experiment is carried out with a series of Gaussian Cartesian sampling patterns but all at the same sampling rate of 0.34. The difference between each sampling pattern is the number of ACS lines.
Code
The MATLAB code of STDLR-SPIRiT can be downloaded here.
Acknowledgments
This work was supported in part by National Key R&D Program of China (2017YFC0108703), National Natural Science Foundation of China (61971361, 61871341, 61811530021, U1632274, 61672335 and 61671399), Natural Science Foundation of Fujian Province of China (2018J06018), Fundamental Research Funds for the Central Universities (20720180056), Science and Technology Program of Xiamen (3502Z20183053), China Scholarship Council, and Xiamen University Nanqiang Outstanding Talents.
References:
[1] J. Hamilton et al., “Recent advances in parallel imaging for MRI,” Progress in Nuclear Magnetic Resonance Spectroscopy, vol. 101, pp. 71–95, 2017.
[2] K. P. Pruessmann et al., “SENSE: Sensitivity encoding for fast MRI,” Magnetic Resonance in Medicine, vol. 42, pp. 952–962, 1999.
[3] M. A. Griswold et al., “Generalized autocalibrating partially parallel acquisitions (GRAPPA),” Magnetic Resonance in Medicine, vol. 47, no. 6, pp. 1202–1210, 2002.
[4] M. Lustig and J. M. Pauly, "SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-space," Magnetic Resonance in Medicine, vol. 64, no. 2, pp. 457-71, 2010.
[5] P.J.Shin et al., “Calibrationless parallel imaging reconstruction based on structured low-rank matrix completion,” Magnetic Resonance in Medicine, vol. 72, no. 4, pp. 959–970, 2014.
[6] K. H. Jin et a.l, “A general framework for compressed sensing and parallel mri using annihilating filter based low-rank hankel matrix,” IEEE Transactions on Computational Imaging, vol. 2, no. 4, pp. 480–495, 2016.
[7] J. P. Haldar, "Low-rank modeling of local k-space neighborhoods (LORAKS) for constrained MRI," IEEE Transaction on Medical Imaging, vol. 33, no. 3, pp. 668-81, 2014.
[8] G. Ongie and M. Jacob, "Off-the-grid recovery of piecewise constant images from few Fourier samples," SIAM Journal on Imaging Sciences, vol. 9, no. 3, pp. 1004-1041, 2016.
[9] X. Qu et al., "Accelerated NMR spectroscopy with low-rank reconstruction," Angewandte Chemie International Edition, vol. 54, no. 3, pp. 852-854, 2015.
[10] J. Ying, et al., "Hankel matrix nuclear norm regularized tensor completion for N-dimensional exponential signals," IEEE Transactions on Signal Processing, vol. 65, no. 14, pp. 3702-3717, 2017.