
Image Reconstruction of Compressed Sensing MRI Using Graph-based Redundant Wavelet Transform (中文,English)
Zongying Lai1,2, Xiaobo Qu2,*, Yunsong Liu2, Di Guo3, Jing Ye2, Zhifang Zhan2, Zhong Chen2,*
1 Department of Communication Engineering and Electronic Science, Fujian Provincial Key Laboratory of Plasma and Magnetic Resonance, Xiamen University, Xiamen 361005, China.
2 Department of Electronic Science, Fujian Provincial Key Laboratory of Plasma and Magnetic Resonance, Xiamen University, Xiamen 361005, China.
3 School of Computer and Information Engineering, Xiamen University of Technology, Xiamen 361024, China.
Xiaobo Qu's Email: quxiaobo <at> xmu.edu.cn or quxiaobo2009 <at> gmail.com.
Citations:
Zongying Lai#, Xiaobo Qu#, Yunsong Liu, Di Guo, Jing Ye, Zhifang Zhan, Zhong Chen. Image reconstruction of compressed sensing MRI using graph-based redundant wavelet transform, Medical Image Analysis, 27: 93-104, 2016. (# denotes co-first authorship)
A free access to full text ( http://authors.elsevier.com/a/1S1Ie4rfPllVGc ) is provided by the publisher that valid for 50 days.
The code is shared at (http://csrc.xmu.edu.cn/project/CS_MRI_GraphWavelet/Toolbox_GBRWT_MRI.zip)
Abstract:
Compressed sensing magnetic resonance imaging(CS-MRI) has shown great capacity for accelerating magnetic resonance imaging if an image can be sparsely represented. How the image is sparsified seriously affects its reconstruction quality. In the present study, a graph-based redundant wavelet transform (GBRWT) is introduced to sparsely represent magnetic resonance images in iterative image reconstructions. Using the l1 norm regularized formulation of the problem solved by an alternating-direction minimization with continuation algorithm, the experimental results demonstrate that the proposed method outperforms several state-of-the-art reconstruction methods in removing artifacts and achieves fewer reconstruction errors on the tested datasets.
Keywords: Compressed sensing, graph, wavelet, MRI, image reconstruction
Methods:
In GBRWT, image is divided to be patches with overlaps. We construct a weighted graph by viewing image patches as vertices and their differences as edges, and the shortest path on the graph minimizes the total difference of all image patches, e.g. the shortest-path-visit makes pixels ranges smoother. Redundant wavelet transform is carried out on the smooth signal (1D) to obtain the sparse representation. An example of patch-graph construction is shown in Fig. 1. The flowchart of GBRWT is illustrated in Fig.2 to illustrate the process of GBRWT-based CS-MRI.

Fig. 1 Patch-based graph
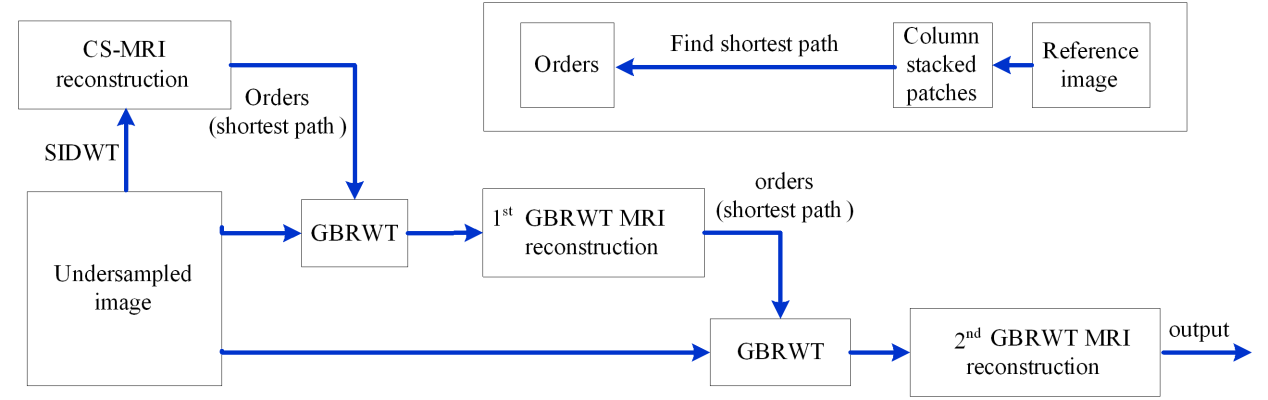
Fig. 2 Flow chart of GBRWT-based MRI reconstruction. The top right block diagram indicates the flow chart for finding the shortest path in patch-graphs to find new orders.
Main result:
1. Reconstruction with phantom

Fig. 3 Reconstructed images and errors in a phantom experiment using Cartesian sampling with 27% data.(a) The fully sampled image;
(b-e) reconstructed images based on WaTMRI, DLMRI, PBDW and GBRWT, respectively; (f)undersampling pattern;(g-j) reconstruction errors (scaled 5x).
2. Reconstruction in vivo data
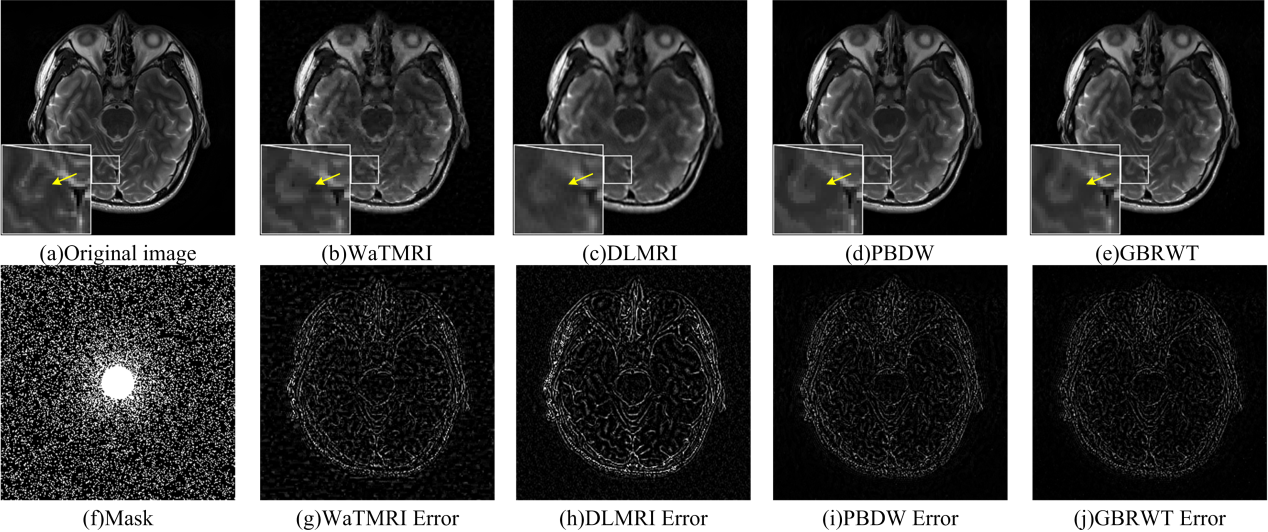
Fig. 4 Reconstructed images and errors with 20% data were used in 2D random sampling.(a) The fully sampled image;
(b-e) reconstructed images based on WaTMRI, DLMRI, PBDW and GBRWT, respectively; (f) undersamplingpattern; (g-j) reconstruction errors (scaled 5x).

Fig. 5 Reconstructed images and errors using Cartesian sampling with 31% data.(a) The fully sampled image;
(b-e) reconstructed images based on WaTMRI, DLMRI, PBDW and GBRWT, respectively; (f) undersampling pattern; (g-j) reconstruction errors (scaled 5x).
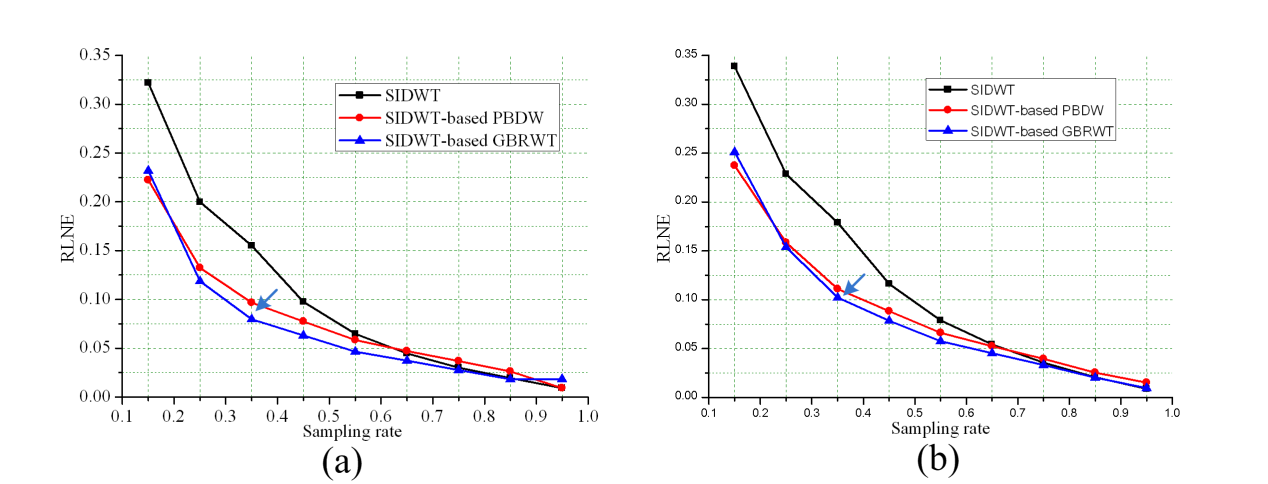
Fig. 6 RLNEs change with the undersampling rate. The reference image of PBDW and GBRWT is the same SIDWT-based reconstructed image.
Conclusion:
In this paper, a new image reconstruction method based on a graph-based redundant wavelet transform is proposed for CS-MRI. This method explores the graph structure to model images and images’ approximate coefficients in each wavelet decomposition level to minimize the total difference of all image patches. The input signal can then be smoothed by new orders estimated by solving the travelling salesman problem in the graph. Wavelet filtering of smoother signals leads to sparser representations of MR images, thus improving the reconstruction. When compared with conventional shift-invariant wavelets and several state-of-the-art CS-MRI image reconstruction methods, including PBDW, DLMRI and WaTMRI, reconstructed images using the proposed method are more consistent with fully sampled images in terms of image intensity and detail. Further improvements can be obtained by optimizing permutation orders trained from the patch-based graph and by further smoothing signals. Finally, parallel processes are expected to reduce the computation time caused by redundancy in future work.
Reference:
[1]. Aelterman, J., Luong, H.Q., Goossens, B., Pižurica, A., Philips, W., 2011. Augmented Lagrangian based reconstruction of non-uniformly sub-Nyquist sampled MRI data. Signal Processing 91, 2731-2742.
[2]. Aharon, M., Elad, M., Bruckstein, A., 2006. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process. 54, 4311-4322.
[3]. Akcakaya, M., Basha, T.A., Chan, R.H., Rayatzadeh, H., Kissinger, K.V., Goddu, B., Goepfert, L.A., Manning, W.J., Nezafat, R., 2012. Accelerated contrast-enhanced whole-heart coronary MRI using low-dimensional-structure self-learning andthresholding. Magn. Reson. Med.67, 1434-1443.
[4]. Akcakaya, M., Basha, T.A., Goddu, B., Goepfert, L.A., Kissinger, K.V., Tarokh, V., Manning, W.J., Nezafat, R., 2011. Low-dimensional-structure self-learning and thresholding: regularization beyond compressed sensing for MRI reconstruction. Magn.Reson. Med.66, 756-767.
[5]. Akcakaya, M., Basha, T.A., Pflugi, S., Foppa, M., Kissinger, K.V., Hauser, T.H., Nezafat, R., 2014. Localized spatio-temporal constraints for accelerated CMR perfusion. Magn. Reson. Med.72, 629-639.
[6]. Baker, C.A., King, K., Dong, L., Leslie, Y., 2011. Translational-invariant dictionaries for compressed sensing in magnetic resonance imaging, 2011 IEEE International Symposium on Biomedical Imaging: From Nano to Macro, 1602-1605.
[7]. Baraniuk, R., Choi, H., Neelamani, R., Ribeiro, V., Romberg, J., Guo, H., Fernandes, F., et.al, 2011. http://dsp.rice.edu/software/rice-wavelet-toolbox.
[8]. Chaari, L., Pesquet, J.C., Benazza-Benyahia, A., Ciuciu, P., 2011. A wavelet-based regularized reconstruction algorithm for SENSE parallel MRI with applications to neuroimaging. Med. Image Anal.15, 185-201.
[9]. Chang, C.H., Ji, J., 2010. Improved compressed sensing MRI with multi-channel data using reweighted l(1) minimization, 2010 Annual International Conference Of the IEEE Engineering In Medicine And Biology Society, 875-878.
[10]. Chen, C., Huang, J.Z., 2014. The benefit of tree sparsity in accelerated MRI. Med. Image Anal.18, 834-842.
[11]. Chen, Y.M., Ye, X.J., Huang, F., 2010. A novel method and fast algorithm for MR image reconstruction with significantly under-sampled data. Inverse Probl. Imaging 4, 223-240.
[12]. Cormen, T.H., Leiserson, C.E., Rivest, R.L., Stein, C., 2001. Introduction to algorithms. The MIT Press, Cambridge, Massachusetts London, England.
[13]. Daubechies, I., Defrise, M., De Mol, C., 2004. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Commun. Pur. Appl. Math.57, 1413-1457.
[14]. Greiser, A., von Kienlin, M., 2003. Efficient k-space sampling by density-weighted phase-encoding. Magn. Reson. Med. 50, 1266-1275.
[15]. Huang, F., Lin, W., Duensing, G.R., Reykowski, A., 2012. k-t sparse GROWL: Sequential combination of partially parallel imaging and compressed sensing in k-t space using flexible virtual coil. Magn. Reson. Med.68, 772-782.
[16]. Jacob, M., 2009. Optimized non-uniform fast Fourier transform (NUFFT) for iterative tomographic reconstruction, 2009. 2009 IEEE International Conference on Acoustics, Speech and Signal Processing, 673-676.
[17]. Jim, J., Zhi-Pei, L., 2001. High resolution cardiac magnetic resonance imaging: a model-based approach, 2001. Proceedings of the 23rd Annual International Conference of the IEEE Engineering in Medicine and Biology Society, 2268-2271.
[18]. Junfeng, Y., Yin, Z., Wotao, Y., 2008. A fast TVL1-L2 minimization algorithm for signal reconstruction from partial Fourier data. CAAM 09-24,Rice university.
[19]. Junfeng, Y., Yin, Z., Wotao, Y., 2010. A fast alternating direction Method for TVL1-L2 signal reconstruction from partial fourier data. IEEE J. Sel. Top. Signal Process.4, 288-297.
[20]. Khalidov, I., Fadili, J., Lazeyras, F., Van De Ville, D., Unser, M., 2011. Activelets: Wavelets for sparse representation of hemodynamic responses. Signal Processing 91, 2810-2821.
[21]. Liu, Y, Cai, J-F, Zhan, Z, Guo, D, Ye, J, Chen, Z., Qu, X., 2015. Balanced sparse model for tight frames in compressed sensing magnetic resonance imaging. PLoS ONE 10. doi:10.1371/journal.pone.0119584.
[22]. Lustig, M., Donoho, D.L., M.Santos, J., Pauly, J.M., 2008. Compressed sensing MRI. IEEE Signal Process. Mag. 72, 72-82.
[23]. Maggioni, M., Katkovnik, V., Egiazarian, K., Foi, A., 2013. Nonlocal transform-domain filter for volumetric data denoising and reconstruction. IEEE Trans. Image Process. 22, 119-133.
[24]. Majumdar, A., Ward, R.K., 2011. An algorithm for sparse MRI reconstruction by Schatten p-norm minimization. Magn. Reson. Imaging 29, 408-417.
[25]. Majumdar, A., Ward, R.K., 2012. Causal dynamic MRI reconstruction via nuclear norm minimization. Magn. Reson. Imaging 30, 1483-1494.
[26]. Majumdar, A., Ward, R.K., Aboulnasr, T., 2013. Non-convex algorithm for sparse and low-rank recovery: Application to dynamic MRI reconstruction. Magn. Reson. Imaging 31, 448-455.
[27]. Ning, B., Qu, X., Guo, D., Hu, C., Chen, Z., 2013. Magnetic resonance image reconstruction using trained geometric directions in 2D redundant wavelets domain and non-convex optimization. Magn. Reson. Imaging 31, 1611-1622.
[28]. Qu, X., Guo, D., Ning, B., Hou, Y., Lin, Y., Cai, S., Chen, Z., 2012. Undersampled MRI reconstruction with patch-based directional wavelets. Magn. Reson. Imaging 30, 964-977.
[29]. Qu, X., Hou, Y., Lam, F., Guo, D., Zhong, J., Chen, Z., 2014. Magnetic resonance image reconstruction from undersampled measurements using a patch-based nonlocal operator. Med. Image Anal. 18, 843-856.
[30]. Qu, X., Zhang, W., Guo, D., Cai, C., Cai, S., Chen, Z., 2010. Iterative thresholding compressed sensing MRI based on contourlet transform. Inverse Probl. Sci. En. 18, 737-758.
[31]. Ram, I., Elad, M., Cohen, I., 2011. Generalized tree-based wavelet transform. IEEE Trans. Signal Process. 59, 4199-4209.
[32]. Ram, I., Elad, M., Cohen, I., 2012. Redundant wavelets on graphs and high dimensional data clouds. IEEE Signal Process. Lett. 19, 291-294.
[33]. Ram, I., Elad, M., Cohen, I., 2013. Image processing using smooth ordering of its patches. IEEE Trans. Image Process. 22, 2764-2774.
[34]. Ravishankar, S., Bresler, Y., 2011. MR image reconstruction from highly undersampled k-space data by dictionary learning. IEEE Trans. Med. Imaging 30, 1028-1041.
[35]. Shensa, M., 1992. The discrete wavelet transform: wedding the atrous and Mallat algorithms. IEEE Trans. Signal Process. 40, 2464-2482.
[36]. Singh, G., Raj, A., Kressler, B., Nguyen, T.D., Spincemaille, P., Zabih, R., Wang, Y., 2011. A fast edge-preserving bayesian reconstruction method for parallel imaging applications in cardiac MRI. Magn. Reson. Med.65, 184-189.
[37]. Skiena, S.S., 2008. The algorithm design manual. Springer, London.
[38]. Tsai, C.M., Nishimura, D.G., 2000. Reduced aliasing artifacts using variable-density k-space sampling trajectories. Magn. Reson. Med. 43, 452-458.
[39]. Wang, Y.-H., Qiao, J., Li, J.-B., Fu, P., Chu, S.-C., Roddick, J.F., 2014. Sparse representation-based MRI super-resolution reconstruction. Measurement 47, 946-953.
[40]. Wang, Y., Ying, L., 2014. Compressed sensing dynamic cardiac cine MRI using learned spatiotemporal dictionary. IEEE Trans. Biomed. Eng. 61, 1109-1120.
[41]. Weller, D.S., Polimeni, J.R., Grady, L., Wald, L.L., Adalsteinsson, E., Goyal, V.K., 2011. Combined compressed sensing and parallel mri compared for uniform and random Cartesian undersampling of k-space, 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 553-556.
[42]. Weller, D.S., Polimeni, J.R., Grady, L., Wald, L.L., Adalsteinsson, E., Goyal, V.K., 2013. Sparsity-promoting calibration for GRAPPA accelerated parallel MRI reconstruction. IEEE Trans. Med. Imaging 32, 1325-1335.
[43]. Xiuquan, J., Jingfei, M., Aref, M., Wiener, E., Zhi-Pei, L., 2003. An improved MRI method for dynamic contrast-enhanced imaging of tumors, 2003. Proceedings of the 25th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, 478-481.
[44]. Ying, D., Ji, J., 2011. Compressive sensing MRI with laplacian sparsifying transform, 2011 IEEE International Symposium on Biomedical Imaging: From Nano to Macro, 81-84.
[45]. Yue, H., Lingala, S.G., Jacob, M., 2012. A fast majorize-minimize algorithm for the recovery of sparse and low-rank matrices. IEEE Trans. Image Process. 21, 742-753.
[46]. Yue, H., Paisley, J., Qin, L., Xinghao, D., Xueyang, F., Xiao-Ping, Z., 2014. Bayesian nonparametric dictionary learning for compressed sensing MRI. IEEE Trans. Image Process. 23, 5007-5019.
[47]. Zhang, S.T., Zhan, Y.Q., Dewan, M., Huang, J.Z., Metaxas, D.N., Zhou, X.S., 2012. Towards robust and effective shape modeling: Sparse shape composition. Med. Image Anal. 16, 265-277.
[48]. Zhou, W., Bovik, A.C., Sheikh, H.R., Simoncelli, E.P., 2004. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 13, 600-612.