A Sparse Model-inspired Deep Thresholding Network for Exponential Signal Reconstruction—Application in Fast Biological Spectroscopy(中文,English)
Zi Wang1, Di Guo2, Zhangren Tu1, Yihui Huang1, Yirong Zhou1, Jian Wang1, Liubin Feng3, Donghai Lin3, Yongfu You4, Tatiana Agback5, Vladislav Orekhov6, Xiaobo Qu1,*
1the Department of Electronic Science, Fujian Provincial Key Laboratory of
Plasma and Magnetic Resonance, National Institute for Data Science in Health and Medicine, Xiamen University, Xiamen, China.
2 the School of Computer and Information Engineering, Xiamen University of Technology, Xiamen, China.
3 the College of Chemistry and Chemical Engineering, Key Laboratory for Chemical Biology of Fujian Province, High-field NMR Center, Xiamen University, Xiamen, China.
4 the China Mobile Group, Xiamen, China.
5 the Department of Molecular Sciences, Swedish University of Agricultural Sciences, Uppsala, Sweden.
6 the Department of Chemistry and Molecular Biology, University of Gothenburg, Gothenburg, Sweden.
* Emails: quxiaobo <at> xmu.edu.cn or quxiaobo2009 <at> gmail.com
Citation
Zi Wang, Di Guo, Zhangren Tu, Yihui Huang, Yirong Zhou, Jian Wang, Liubin Feng, Donghai Lin, Yongfu You, Tatiana Agback, Vladislav Orekhov, Xiaobo Qu, A Sparse Model-inspired Deep Thresholding Network for Exponential Signal Reconstruction—Application in Fast Biological Spectroscopy, IEEE Transactions on Neural Networks and Learning Systems, doi: 10.1109/TNNLS.2022.3144580, 2022.
Synopsis
Ast data acquisition of exponentials is widely used in many signal processing applications: Telecommunication, fluorescence microscopy, analog-to-digital conversion, medical imaging, geoscience, biological nuclear magnetic resonance (NMR) spectroscopy, and so on. The non-uniform sampling (NUS) has been a popular technique to enable fast acquisition by reducing the amount of acquired data. Since the data is undersampled, there are lots of artifacts in the spectrum obtained by Fourier transform. Thus, faithful reconstruction from undersampled exponential signals is one of the frontiers and highly significant problem in signal processing.
Deep learning has shown astonishing potential in this field but many existing problems, such as lack of robustness and explainability, greatly limit its applications. Hence, the question remains, how to design a deep neural network suitable for reconstructing exponential signals, and achieve more robust performance and low computational cost?
Main Context
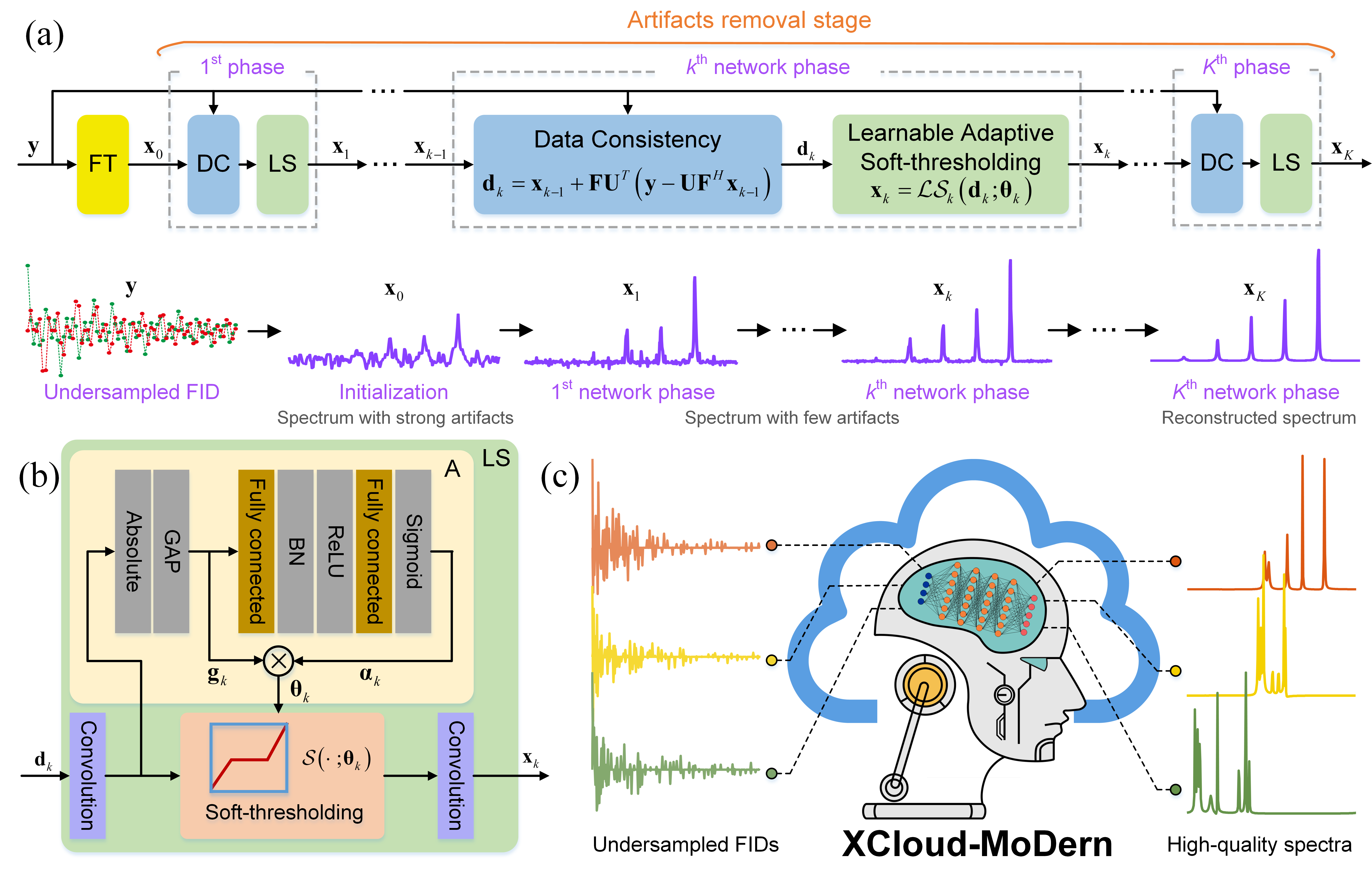
In this work, by combining merits of the sparse model-based optimization method and data-driven deep learning, we propose a deep learning architecture for spectra reconstruction from undersampled data, called MoDern (Fig. 1). It follows the iterative reconstruction in solving a sparse model to build the neural network and we elaborately design a learnable soft-thresholding to adaptively eliminate the spectrum artifacts introduced by undersampling. Extensive results on both synthetic and biological data show that MoDern enables more robust, high-fidelity, and ultra-fast reconstruction than the state-of-the-art methods. Remarkably, MoDern has a small number of network parameters and is trained on solely synthetic data while generalizing well to biological data in various scenarios. Furthermore, we extend it to an open-access and easy-to-use cloud computing platform (XCloud-MoDern), contributing a promising strategy for further development of biological applications.

Fig. 1. An overview of MoDern and XCloud-MoDern. (a) The recursive MoDern framework that alternates between the data consistency (DC) module and the learnable adaptive soft-thresholding (LS) module. With the increase of the network phase, artifacts are gradually removed, and finally a high-quality reconstructed spectrum can be obtained. (b) The detailed structure of the learnable adaptive soft-thresholding (LS) module and threshold adaptive-setting (A) module. (c) The developed artificial intelligence cloud computing platform (XCloud-MoDern) for processing multi-dimensional NMR spectra. Note: “FT” is the Fourier transform.
We evaluate the reconstruction performance on synthetic data under different scenarios, such as different number of exponentials (spectra peaks) and NUS densities. For each (NUS density, number of exponentials) pair, 100 Monte Carlo trails are conducted. We set two error thresholds (RLNE=0.05 and 0.02), which are represented by white and red lines, respectively. The corresponding energy loss is 0.25% and 0.04%, which can be considered as small and very small reconstruction error. Fig. 2 shows that MoDern can better handle exponential signal reconstructions with large number of exponentials or low NUS density. The region below the red line, denoting a lower reconstruction error (RLNE) than 0.02, is significantly larger for MoDern than three compared methods. If we relax the acceptable energy loss to 0.25% (white line), the regions of three compared methods obviously become large, whereas MoDern consistently owns the largest region. For example, when NUS density is 15%, MoDern enables the reliable reconstruction of 9 exponentials, while CS, DLNMR, and DHMF allow 2, 4, and 7 exponentials, respectively. These observations imply that MoDern provides better reconstructions than compared methods in general signal processing.
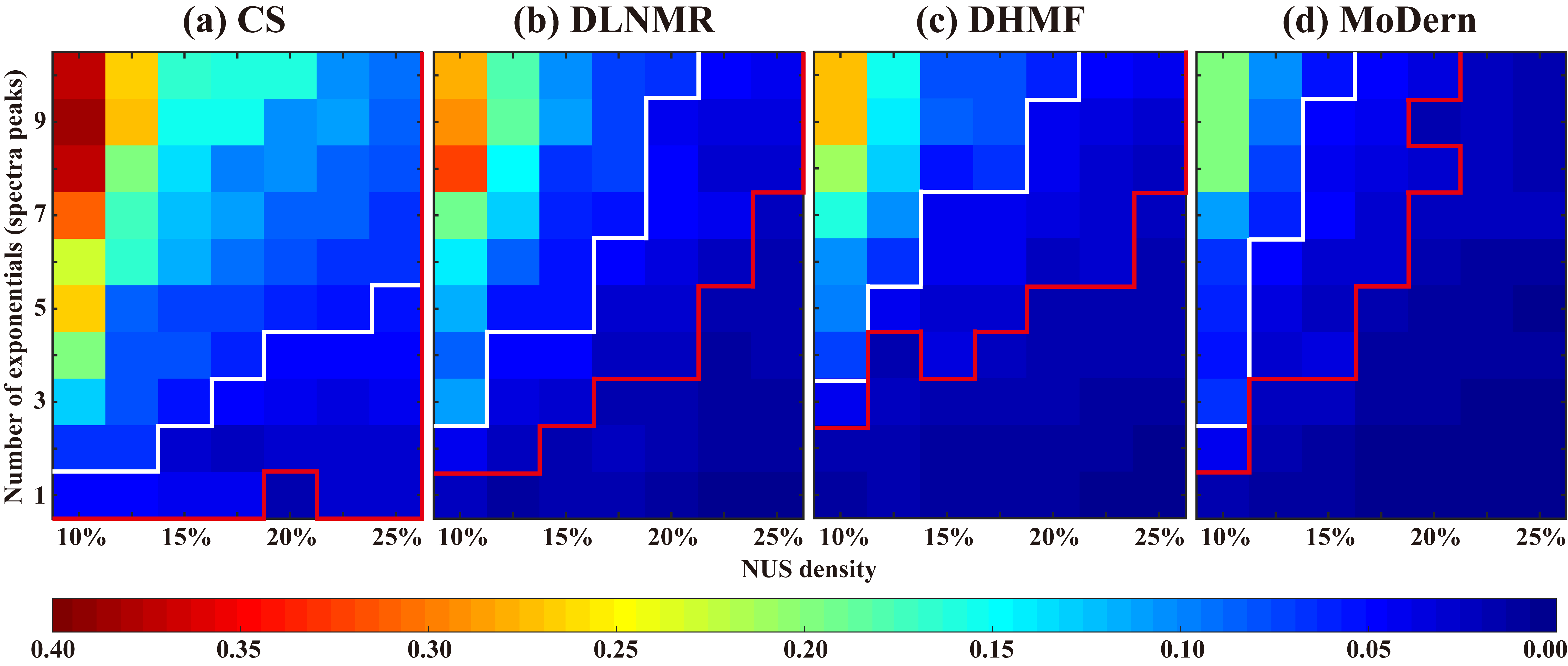
Fig. 2. Reconstruction of the synthetic data under different scenarios. (a)-(d) are average reconstruction errors, RLNEs of CS, DLNMR, DHMF and MoDern, respectively. Note: Each color reflects the average RLNEs over 100 Monte Carlo trials with different sampling masks. Red (or white) line indicates an empirical boundary where the error threshold RLNE is 0.02 (or 0.05). Below the boundary, the reconstruction error of the region is less than the error threshold.
Multi-dimensional biological NMR spectroscopy serves an indispensable and widely used biological tool in modern biology, chemistry, and life science, but suffers from the long data acquisition time. Given the importance and time bottleneck of biological spectroscopy, fast sampling and reliable reconstruction is highly expected. Therefore, we further extend the proposed MoDern to an important application of exponential signal reconstruction -- fast multidimensional biological spectroscopy.
A key factor that limits wide usage of existing DL for NMR spectra reconstruction is the lack of robustness and versatility. They cannot overcome the mismatch between training and test data in practical applications. It means that NMR researchers need to spend numerous times on re-training networks to handle various reconstruction tasks of different NUS densities, which is obviously unacceptable. Here, we evaluate the reconstruction performance under mismatch on two NMR data (a 2D 1H-15N HSQC spectrum of CD79b and a 3D HNCACB spectrum of GB1-HttNTQ7). In Fig. 3, MoDern and DLNMR are trained using 15% (or 10%) NUS density dataset, to reconstruct 2D (or 3D) NMR data under different NUS densities. MoDern maintains the high-quality and significantly better than DLNMR reconstruction performance when the NUS density of spectra significantly deviates from the level used in the training (Figs. 3(a)(e)). We want to point out that the observed phenomenon of MoDern is highly aligned to model-based methods and follows our intuition: The higher NUS densities, the better reconstruction qualities. On the contrary, with more given sampled points if the mismatch exists, DLNMR may even show obvious intensity distortions, artifacts, and lower R2 (Fig. 3(c)(g)).
More excellent performance of MoDern in other challenging data and quantitative measurement of relative concentration of metabolites can be found in the full-length paper.
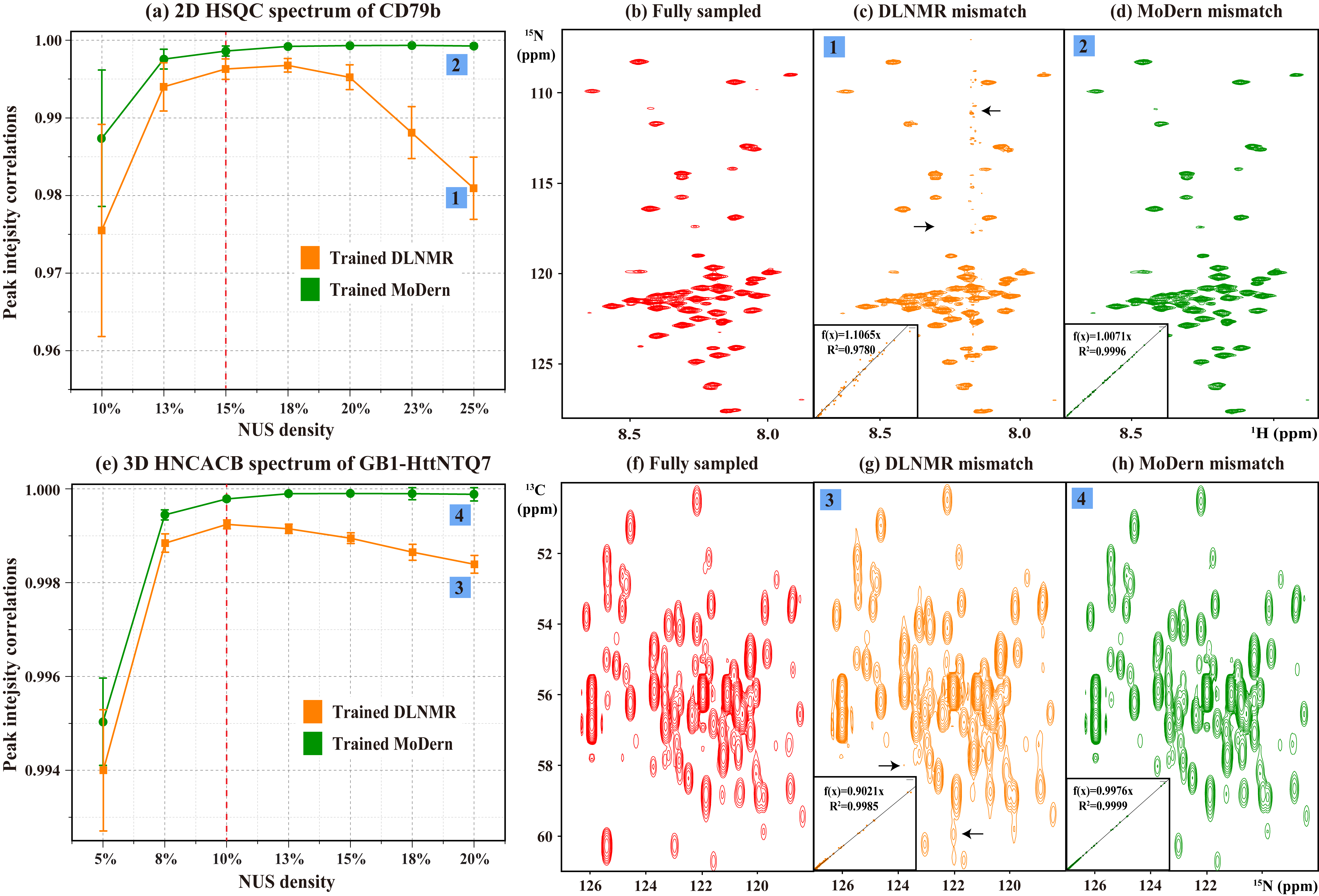
Fig. 3. Reconstruction of 2D and 3D NMR data under mismatch in DL. (a) R2 between the fully sampled 2D HSQC spectrum of CD79b and reconstructed spectra. (b)-(d) are the fully sampled spectrum, the typical reconstructions by DLNMR and MoDern, respectively. (e) R2 between the fully sampled 3D HNCACB spectrum of GB1-HttNTQ7 and reconstructed spectra. (f)-(h) are sub-regions of the projections on 13C-15N planes of the fully sampled spectrum, the typical reconstructions by DLNMR and MoDern, respectively. Note: The dashed red lines in (a) and (e) indicate the NUS densities that the networks are trained for. The insets of (c)(d)(g)(h) show R2. The average and standard deviations of correlations in (a) and (e) are computed over 100 and 50 Monte Carlo trials with different sampling masks, respectively. The obvious intensity distortions and artifacts are marked with the black arrow.
Shared Materials
Cloud computing platform (XCloud-MoDern) and shared data
Acknowledgements
This work was supported in part by the National Natural Science Foundation of China under grants 62122064, 61971361, 61871341, and 61811530021, the Natural Science Foundation of Fujian Province of China under grant 2021J011184, the National Key R&D Program of China under grant 2017YFC0108703, the Xiamen University Nanqiang Outstanding Talents Program, the Swedish Research Council under grant 2015–04614, and the Swedish Foundation for Strategic Research under grant ITM17-0218.
References
[1] X. Qu, M. Mayzel, J.-F. Cai, Z. Chen, and V. Orekhov, “Accelerated NMR spectroscopy with low-rank reconstruction,” Angew. Chem. Int. Ed., vol. 54, no. 3, pp. 852-854, 2015.
[2] J. Ying, J.-F. Cai, D. Guo, G. Tang, Z. Chen, and X. Qu, “Vandermonde factorization of Hankel matrix for complex exponential signal recovery—Application in fast NMR spectroscopy,” IEEE Trans. Signal Process., vol. 66, no. 21, pp. 5520-5533, 2018.
[3] V. Jaravine, I. Ibraghimov, and V. Yu Orekhov, “Removal of a time barrier for high-resolution multidimensional NMR spectroscopy,” Nature Met., vol. 3, no. 8, pp. 605-607, 2006.
[4] M. Mobli and J. C. Hoch, “Nonuniform sampling and non-Fourier signal processing methods in multidimensional NMR,” Prog. Nucl. Magn. Reson. Spectrosc., vol. 83, pp. 21-41, 2014.
[5] Y. Huang, J. Zhao, Z. Wang, D. Guo, and X. Qu, “Exponential signal reconstruction with deep Hankel matrix factorization,” IEEE Trans. Neural Netw. Learn. Syst., 2021, DOI: 10.1109/TNNLS.2021.3134717.
[6] K. Kazimierczuk and V. Y. Orekhov, “Accelerated NMR spectroscopy by using compressed sensing,” Angew. Chem. Int. Ed., vol. 50, no. 24, pp. 5556-5559, 2011.
[7] T. Qiu, Z. Wang, H. Liu, D. Guo, and X. Qu, “Review and prospect: NMR spectroscopy denoising and reconstruction with Low-Rank Hankel matrices and tensors,” Magn. Reson. Chem., vol. 59, pp. 324-345, 2021.
[8] X. Qu et al., “Accelerated nuclear magnetic resonance spectroscopy with deep learning,” Angew. Chem. Int. Ed., vol. 59, no. 26, pp. 10297-10300, 2020.
[9] Y. LeCun, Y. Bengio, and G. Hinton, “Deep learning,” Nature, vol. 521, pp. 436-444, 2015.
[10] D. Chen, Z. Wang, D. Guo, V. Orekhov, and X. Qu, “Review and prospect: Deep learning in nuclear magnetic resonance spectroscopy,” Chem. Eur. J., vol. 26, no. 46, pp. 10391-10401, 2020.
[11] Z. Wang et al., “One-dimensional deep low-rank and sparse network for accelerated MRI," arXiv:2112.04721, 2021.
[12] J. Hoch and A. Stern, NMR Data Processing. 1996.
[13] D. L. Donoho, “De-noising by soft-thresholding,” IEEE Trans. Inf. Theory, vol. 41, no. 3, pp. 613-627, 1995.