Accelerated MRI Reconstruction with Separable and Enhanced Low-Rank Hankel Regularization(中文，English)

Xinlin Zhang¹, Hengfa Lu²,Di Guo³, Zongying Lai⁴, Huihui Ye⁵, Xi Peng⁶, Bo Zhao⁷, Xiaobo Qu^1,*

¹Biomedical Intelligent Cloud R&D Center, Department of Electronic Science, National Institute for Data Science in Health and Medicine, Xiamen University, Xiamen, China.
² the Department of Biomedical Engineering, University of Texas at Austin, Austin, USA.
³ the School of Computer and Information Engineering, Xiamen University of Technology, Xiamen, China.
⁴ the School of Information Engineering, Jimei University, Xiamen, China.
⁵ the State of Key Laboratory of Modern Optical Instrumentation, College of Optical Science and Engineering, Zhejiang University, Hangzhou, China.
⁶ the Department of Radiology, Mayo Clinic, Rochester, USA.
⁷ the Department of Biomedical Engineering, Oden Institute for Computational Engineering and Sciences, University of Texas at Austin, Austin, USA.
^* Email: quxiaobo <at> xmu.edu.cn

Citation

Xinlin Zhang, Hengfa Lu, Di Guo, Zongying Lai, Huihui Ye, Xi Peng, Bo Zhao, Xiaobo Qu, Accelerated MRI Reconstruction With Separable and Enhanced Low-Rank Hankel Regularization, IEEE Transactions on Medical Imaging, vol. 41, no. 9, pp.2486-98, 2022.

Synopsis

Magnetic resonance imaging (MRI) is a nonradioactive, non-invasive imaging technique that is able to provide multi-contrast images and permit excellent soft tissue images. However, the long acquisition time has always been one of the bottlenecks in the industry. Sparse sampling greatly reduces sampling time, but it requires to reconstruct images from undersampled data. In recent years, our team proposed a novel approach to reconstruct MRI image by exploring the Hankel low rank properties of k space. The proposed method has the ability to yield robust reconstruction and maintain low reconstruction error. However, this method needs to construct a huge block Hankel matrix, leading to considerable computational time and memory consumption in reconstruction. How to reconstruct MRI images quickly and better is still an urgent problem to be solved.

In this work, we proposed a separable low-rank Hankel matrix image reconstruction method, which dramatically shorten reconstruction time, and has been successfully applied in parallel imaging and quantitative imaging. Our retrospective in-vivo results indicate that the proposed approaches permits the lowest reconstruction error with a fast reconstruction.

Main Context

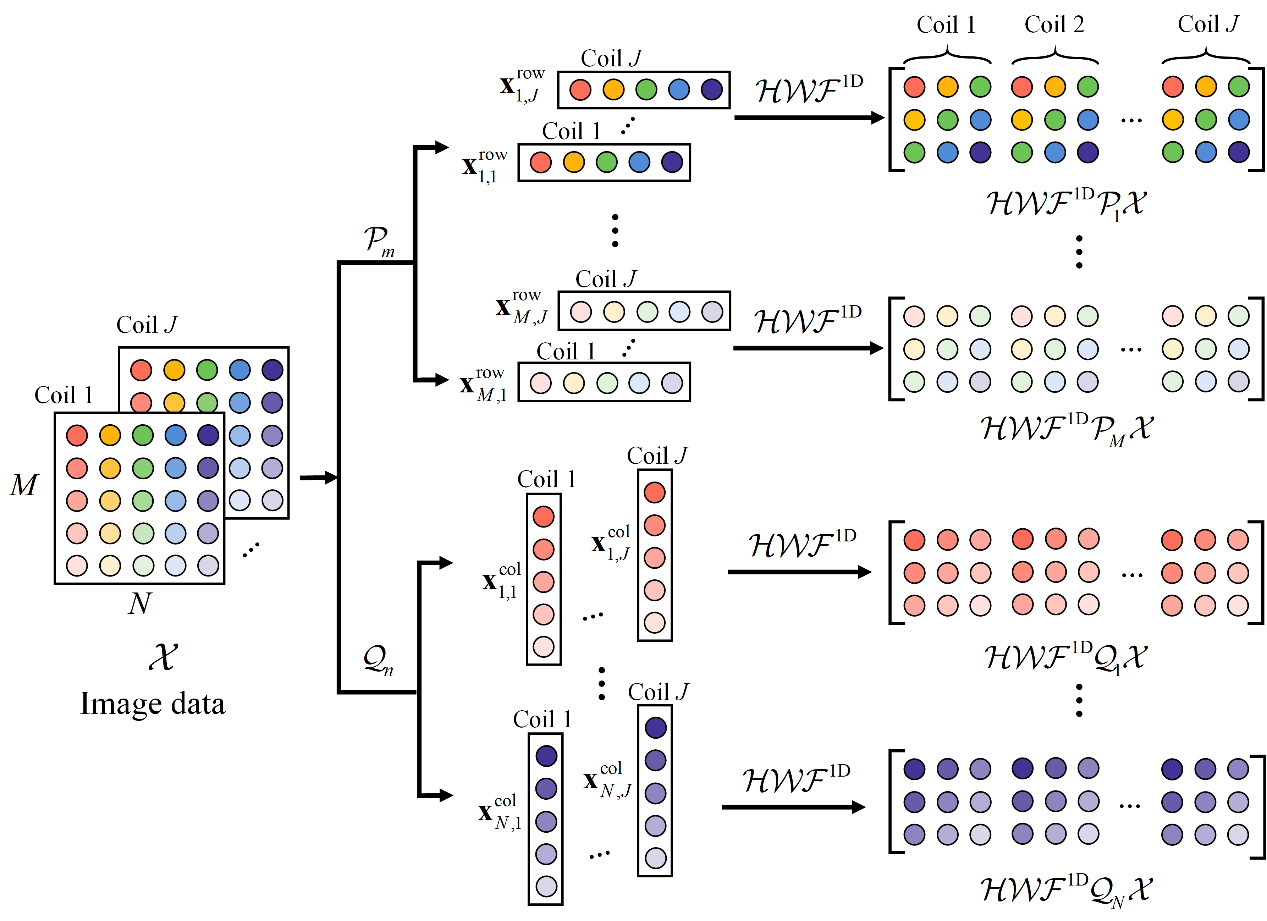
In order to speed up the reconstruction, this work proposed to construct multiple small-scale Hankel matrices (Fig. 1) by separating the rows/columns of the k space. The separable model significantly reduces the computation time (which is 4% computation time of STDLR-SPIRiT). However, it did not make use of the correlations that exist between rows and columns or columns and columns, resulting in increase of reconstruction errors. We further introduced prior knowledge such as k-space self-consistency and virtual coils to improve the reconstruction. Real data experiments show that the separable model enable to introduce prior flexibly without obviously increasing the computation. The proposed separable model can be extended to parallel imaging and quantitative imaging, and successfully achieved 8× undersampling and one-minute reconstruction of T2 mapping imaging. It provides strategy for accurate and rapid quantitative imaging of tumors.

Fig. 1. Illustration of constructing separable Hankel matrices in SHLR.

In this work, we attempted to alleviate the huge computational complexity and lengthy reconstruction time problems of the state-of-the-art structural low-rank approaches. To reduce the computational time, we proposed a separable Hankel lowrank reconstruction method, named SHLR, to enforce the Hankel low-rankness of each row and each column of the signal of interest. But this way to enforce the low-rankness is sub-optimal compared to block Hankel methods, though holds the advantage of swift runtime. To enhance the performance of SHLR, we introduced prior information. For parallel imaging, we explored the correlation between rows/columns and the virtual coil technique, and proposed the SHLR-SV model. Regarding parameter imaging, we assumed that the signal intensity along the parameter dimension varies in an exponential way. We enforced the exponential property and virtual coil technique and proposed a model named SHLR-VP for accelerating parameter imaging.

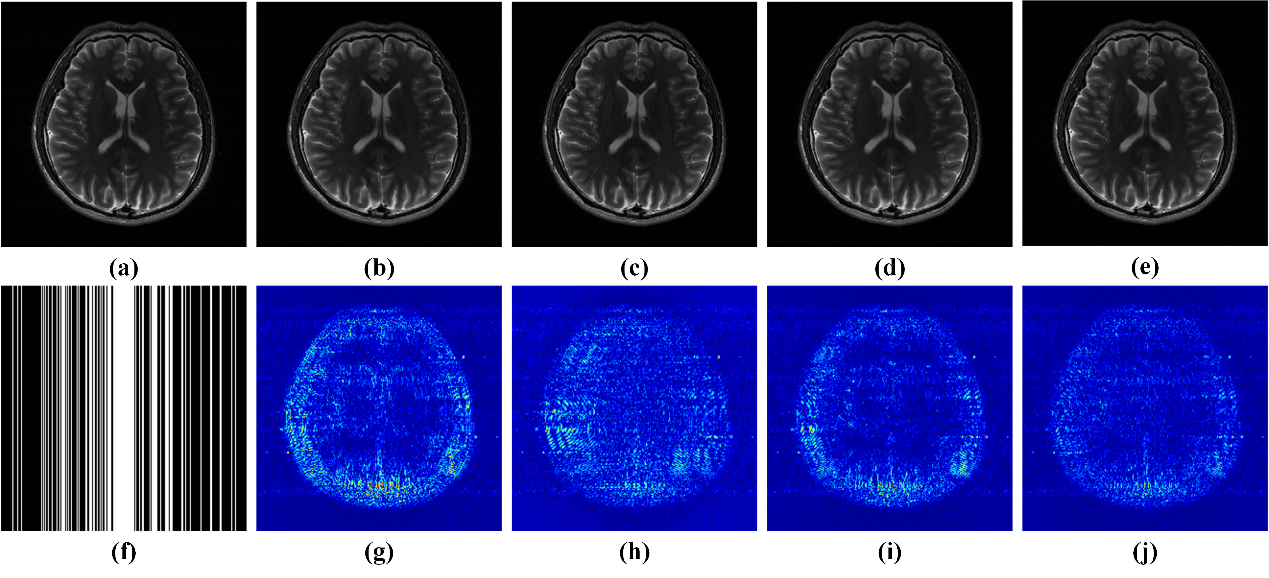
Fig. 2. Parallel imaging reconstruction results and errors under Cartesian sampling pattern with a sampling rate of 0.34. (a) An SSOS image of fully sampled data; (b-e) SSOS images of reconstructed results by ℓ1-SPIRiT, AC-LORAKS, STDLR-SPIRiT and SHLR-SV, respectively; (f) the Cartesian undersampling pattern; (g-j) the reconstruction error distribution (12.5×) corresponding to reconstructed image above them.

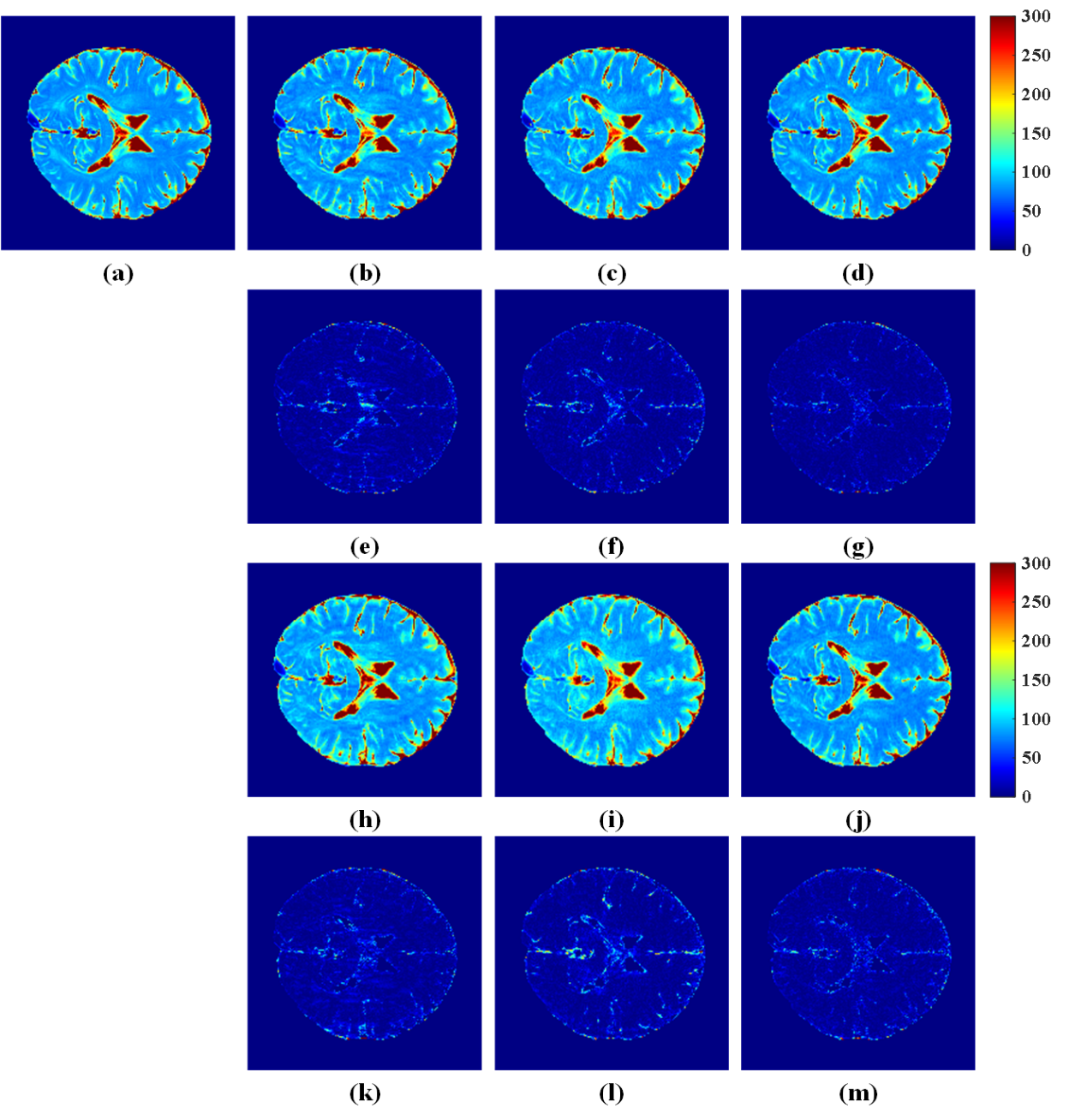
Fig. 3. T2 mapping reconstruction results and errors under two undersampling patterns. (a) T2 map of fully sampled data; (b-d) T2 maps of reconstructed results at reduction factors R=6 by MORASA, ALOHA, and SHLR-VP, respectively; (h-j) T2 maps of reconstructed results at R=8 by MORASA, ALOHA, and SHLR-VP, respectively; (e-g) and (k-m) the reconstruction error distribution (6×) corresponding to reconstructed image above them. Note: the RLNE/MSSIM of (b-d) are 0.0978/0.9891, 0.0959/0.9883, and 0.0796/0.9922, respectively, and the RLNE/MSSIM of (h-j) are 0.1262/0.9831, 0.1386/0.9775, and 0.0980/0.9880, respectively.

Experimental in-vivo results showed that the proposed two approaches enable better results than the state-of-the-art methods. Notably, the proposed methods allow reconstructions with smaller errors and faster reconstruction speed. The proposed approach requires only 4% of the state-of-the-art STDLR-SPIRiT runtime for parallel imaging reconstruction, and achieves the fastest computational speed in quantitative imaging.

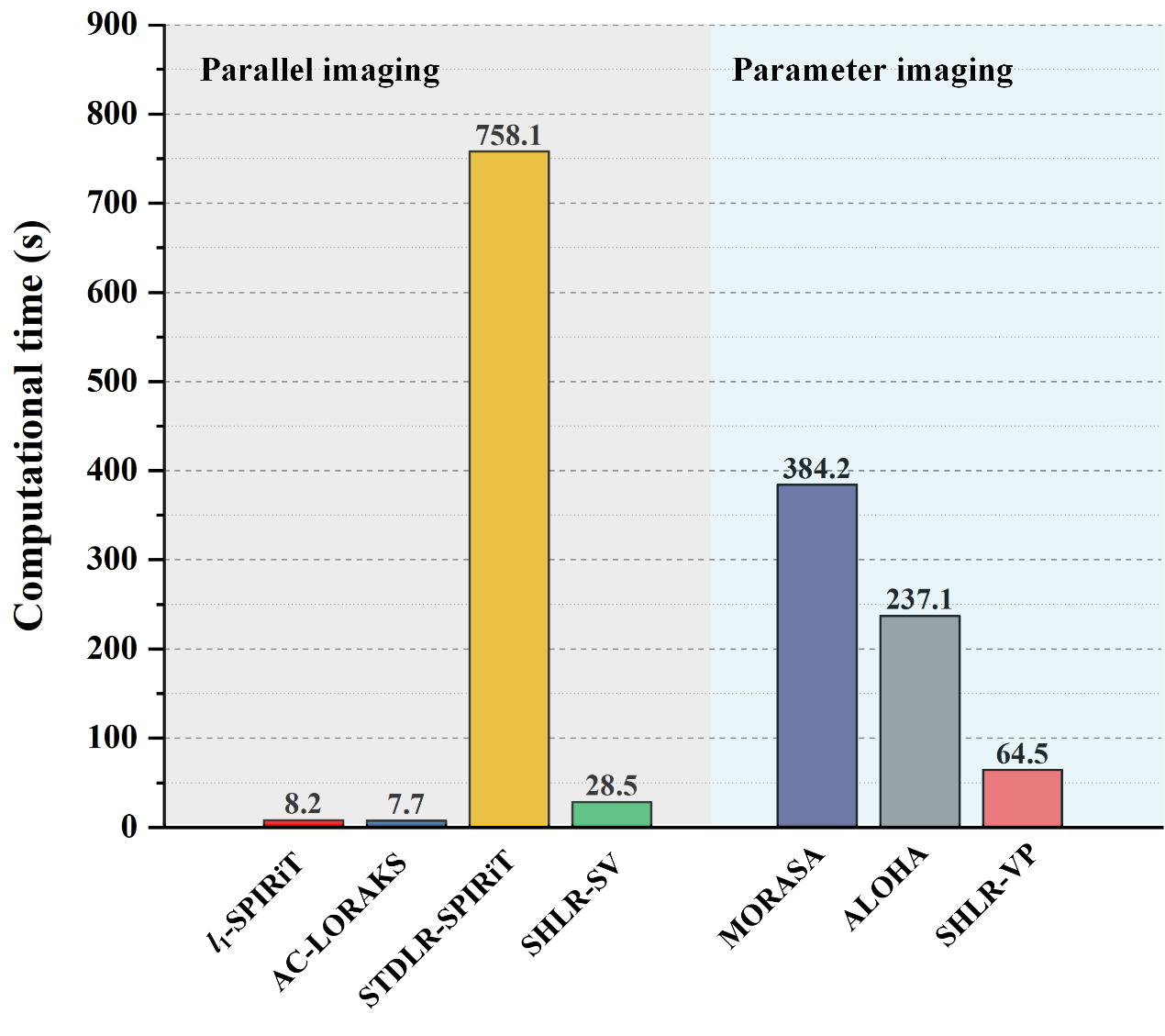
Fig. 4. The computational time of different methods in parallel imaging and parameter imaging.

Code

The MATLAB code of SHLR-SV and SHLR-VP can be downloaded here.

Acknowledgements

This work was supported in part by the National Natural Science Foundation of China under Grant 61971361, Grant 62122064, Grant 61871341, and Grant 61901188; in part by the Natural Science Foundation of Fujian Province of China under Grant 2021J011184; in part by the National Key Research and Development Program of China under Grant 2017YFC0108703; in part by the Xiamen University Nanqiang Outstanding Talents Program; and in part by the China Scholarship Council under Grant 202006310142.

References

[1] J. Hamilton, D. Franson, and N. Seiberlich, “Recent advances in parallel imaging for MRI,” Progress in Nuclear Magnetic Resonance Spectroscopy, vol. 101, pp. 71–95, 2017.
[2] M. Lustig and J. M. Pauly, “SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-space,” Magnetic Resonance in Medicine, vol. 64, no. 2, pp. 457–71, 2010.
[3] J. P. Haldar, “Autocalibrated LORAKS for fast constrained MRI reconstruction,” in 2015 IEEE 12th International Symposium on Biomedical Imaging (ISBI), 2015, pp. 910–913.
[4] X. Zhang, D. Guo, Y. Huang, Y. Chen, L. Wang, F. Huang, Q. Xu, and X. Qu, “Image reconstruction with low-rankness and self-consistency of k-space data in parallel MRI,” Medical Image Analysis, vol. 63, p. 101687, 2020.
[5] X. Peng, L. Ying, Y. Liu, J. Yuan, X. Liu, and D. Liang, “Accelerated exponential parameterization of T2 relaxation with model-driven low rank and sparsity priors (MORASA),” Magnetic Resonance in Medicine, vol. 76, no. 6, pp. 1865–1878, 2016.
[6] D. Lee, K. H. Jin, E. Y. Kim, S.-H. Park, and J. C. Ye, “Acceleration of MR parameter mapping using annihilating filter-based low rank Hankel matrix (ALOHA),” Magnetic Resonance in Medicine, vol. 76, no. 6, pp. 1848–1864, 2016.