Sparse MRI Reconstruction Using Multi-contrast Image Guided
Graph Representation( [Chinese] )
Zongying Lai1,2, Xiaobo Qu2,*, Hengfa Lu2, Xi
Peng3 , Di Guo3, Yu Yang2, Gang
Guo5, Zhong Chen2,*
1Department of Communication Engineering, Xiamen University, Xiamen
361005, China;
2Department of Electronic Science, Xiamen University, Xiamen 361005,
China;
3Paul C. Lauterbur Research Centre for Biomedical Imaging, Shenzhen Institutes of Advanced Technology, Shenzhen
518055, China.
4School of Computer and Information Engineering, Fujian Provincial
University Key Laboratory of Internet of Things Application Technology, Xiamen
University of Technology, Xiamen 361024, China
5Department of Radiology, Xiamen 2nd Hospital, Xiamen
361021, China
Citations: Zongying Lai, Xiaobo Qu, Hengfa Lu, Xi
Peng, Di Guo, Yu Yang, Gang Guo, Zhong Chen. Sparse MRI reconstruction using
multi-contrast image guided graph representation, Magnetic Resonance Imaging, 43:95-104, 2017.
Access
to full text (
https://doi.org/10.1016/j.mri.2017.07.009)
The code is shared at ( http://csrc.xmu.edu.cn/project/CS_MRI_GraphWavelet_Multicontrast/Toolbox_GBRWT_Multicontrast_MRI.zip
)
Contact :
quxiaobo<|at|>xmu.edu.cn
Abstract:
Accelerating the imaging speed
without sacrificing image structures plays an important role in magnetic
resonance imaging. Under-sampling the k-space data and reconstructing the image
with sparsity constraint is one efficient way to reduce the data acquisition
time. However, achieving high acceleration factor is challenging since image
structures may be lost or blurred when the acquired information is not
sufficient. Therefore, incorporating extra knowledge to improve image
reconstruction is expected for highly accelerated imaging. Fortunately,
multi-contrast images in the same region of interest are usually acquired in
magnetic resonance imaging protocols. In this work, we propose a new approach
to reconstruct magnetic resonance images by learning the prior knowledge from
these multi-contrast images with graph-based wavelet representations. We
further formulate the reconstruction as a bi-level optimization problem to
allow misalignment between these images. Experiments on realistic imaging
datasets demonstrate that the proposed approach improves the image
reconstruction significantly and is practical for real world application since
patients are unnecessarily to stay still during successive reference image
scans.
KEYWORDS: Magnetic resonance
imaging; image reconstruction; sparse representation; multi-contrast;
misalignment.
Methods:
In
this sparse MRI reconstruction method using multi-contrast image guided graph
representation, multi-contrast images are firstly registered to each other to
resist misalignment; then, graph representation is learned from a fully
sampled-and-registered multi-contrast image by viewing image patches as
vertices and their differences as edges, via a shortest-path-visit to makes
pixels ranges smoother, and finally form the graph representation (multi-contrast
image guided graph-based redundant wavelet transform, MGBRWT). The
MGBRWT is used as the sparse representation to do sparse reconstruction of
other contrast MRI images. The flowchart of sparse reconstruction of using MGBRWT
is illustrated in Fig.1.
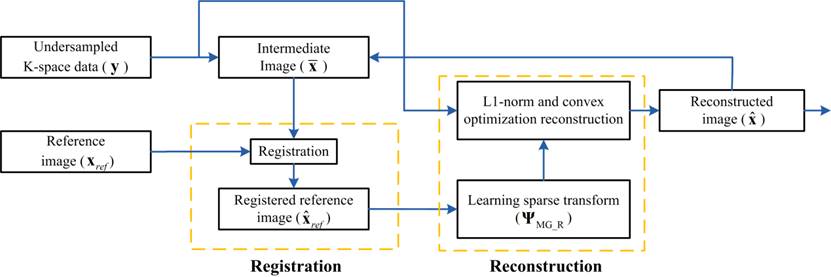
Fig. 1 Flowchart of this work.
Main
result:
1.
Sparse
MRI reconstruction methods comparisons on in
vivo data.
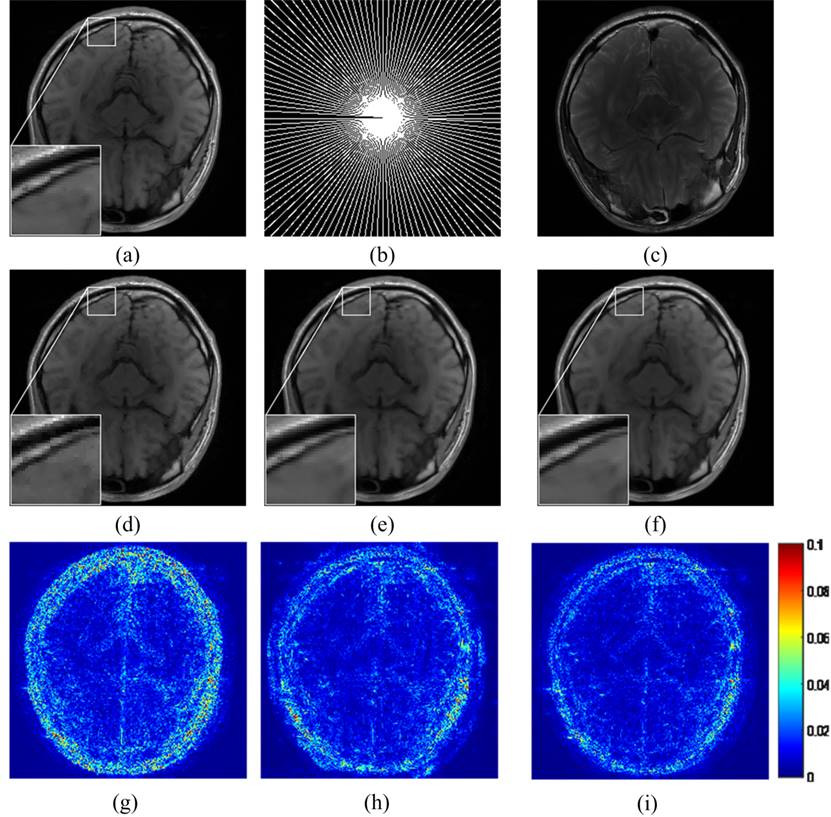
Fig. 2 MRI reconstruction with pseudo radial sampling. The (a-c) are
the ground-truth, pseudo radial under-sampling with 25% data, and
reference, respectively. (d-f) are the reconstructed images using BCS[42,43],
PANO[41] and the proposed method; (g-i) magnitude errors
using BCS, PANO and the proposed method. Note: (d-f) achieved RLNEs 0.071, 0.056 and 0.048,
respectively; (d-f) achieved MSSIMs 0.9508, 0.9581 and 0.9673, respectively.
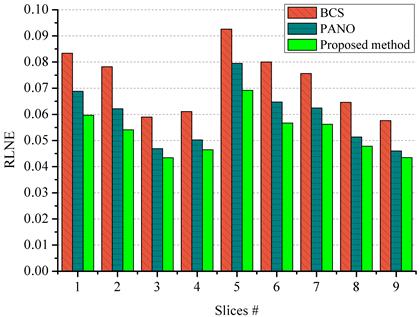
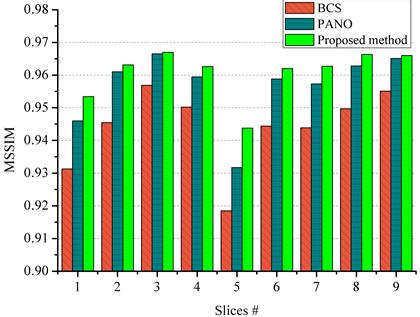
Fig. 3 Reconstruction with
more MRI slices. The (a) and (b) are reconstructed RLNEs and MSSIMs with 20% under-sampled
data.
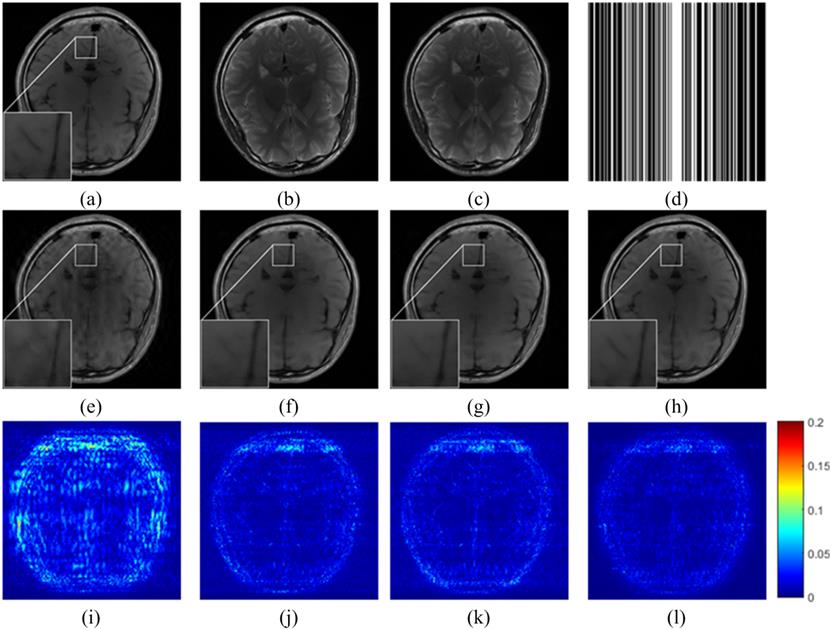
Fig. 4 Reconstructed
images using other typical methods. (a) The fully sampled target image; (b) is
the unregistered reference image in another contrast; (c) is the registered
reference image; (d) denotes the under-sampling pattern; (e-h) are
reconstructed images using the l 21-norm[48],
TLMRI[15], DLMRI[9] and the proposed method with the registered another
contrast image in (c) as the reference image. (i-l) are reconstructed errors of
l 21-norm,
TLMRI, DLMRI reconstructions and the proposed method.
2. The
advantages of multi-contrast image as prior
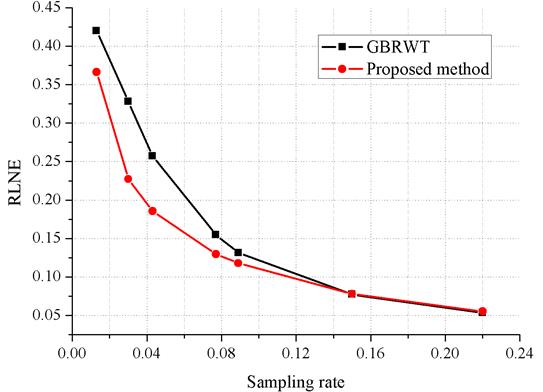
Fig. 5 Proposed method vs.
original GBRWT-based MRI reconstruction[16]. The target and reference images
are same with that shown in Fig. 2 in the full paper.
Conclusion:
A sparse MRI image reconstruction method by
incorporating prior information from multi-contrast reference images is
proposed in this work. The prior information is embedded into the graph
wavelet-based image sparse representation learnt from the reference image and
this information updated with better accuracy by iteratively registering the
reference image to the target one. Results on realistic MRI images implies that
incorporating multi-contrast images can significantly improve the
reconstruction and the iteration between registration and reconstruction is
necessary when the acquired is very limited. The proposed approach would be
meaningful for highly accelerated MRI imaging
References
[1] H. Jung, K. Sung, K.
S. Nayak, E. Y. Kim, and J. C. Ye, "k-t FOCUSS: a general compressed
sensing framework for high resolution dynamic MRI," Magn Reson Med. 61 (2009) 103-16.
[2] T.
Zhang, J. Y. Cheng, A. G. Potnick, R. A. Barth, M. T. Alley, M. Uecker, et al.,
"Fast pediatric 3D free-breathing abdominal dynamic contrast enhanced MRI
with high spatiotemporal resolution," J
Magn Reson Imaging, 41 (2015), 460-73.
[3] Y.
Hu and G. H. Glover, "Increasing spatial coverage for high-resolution
functional MRI," Magn. Reson. Med., 61 (2009), 716-722.
[4] M.
Lustig, D. Donoho, and J. M. Pauly, "Sparse MRI: The application of
compressed sensing for rapid MR imaging," Magn. Reson. Med. 58 (2007)
1182-95.
[5] M.
Lustig, D. L. Donoho, J. M.Santos, and J. M. Pauly, "Compressed sensing
MRI," IEEE Signal Proc. Mag. 72 (2008) 72-82.
[6] Y.
Yang, F. Liu, W. Xu, and S. Crozier, "Compressed sensing MRI via two-stage
reconstruction," IEEE Trans. Bio-Med
Eng. 62 (2015) 110-118.
[7] S.
G. Lingala and M. Jacob, "Blind compressive sensing dynamic MRI," IEEE Trans. Med. Imaging 32 (2013)
1132-1145.
[8] X.
Ye, Y. Chen, and F. Huang, "Computational acceleration for MR image
reconstruction in partially parallel imaging," IEEE Trans. Med. Imaging 30 (2011) 1055-1063.
[9] S.
Ravishankar and Y. Bresler, "MR image reconstruction from highly
undersampled k-space data by dictionary learning," IEEE Trans. Med. Imaging 30 (2011) 1028-1041.
[10] X.
Qu, D. Guo, B. Ning, Y. Hou, Y. Lin, S. Cai,
et al., "Undersampled MRI reconstruction with patch-based directional
wavelets,"Magn.
Reson. Imaging 30 (2012)
964-977.
[11] Z.
Zhan, J. F. Cai, D. Guo, Y. Liu, Z. Chen, and X. Qu, "Fast multiclass
dictionaries learning wth geometrical directions in MRI reconstruction," IEEE Trans. Bio-Med. Eng. 63 (2016)
1850-1861.
[12] Q.
Liu, S. Wang, K. Yang, J. Luo, Y. Zhu, and D. Liang, "Highly undersampled
magnetic resonance image reconstruction using two-Level Bregman method with
dictionary updating," IEEE Trans.
Med. Imaging 32 (2013) 1290-1301.
[13] A.
Majumdar, "Motion predicted online dynamic MRI reconstruction from
partially sampled k-space data,"Magn.
Reson Imaging 31 (2013) 1578-1586.
[14] R. W.
Liu, L. Shi, W. Huang, J. Xu, S. C. H. Yu, and D. Wang, "Generalized total
variation-based MRI Rician denoising model with spatially adaptive
regularization parameters,"Magn.
Reson Imaging 32 (2014) 702-720.
[15] S.
Ravishankar and Y. Bresler, "Efficient Blind Compressed Sensing Using
Sparsifying Transforms with Convergence Guarantees and Application to
MRI," Mathematics, 2 (2015),
294-309.
[16] Z.
Lai, X. Qu, Y. Liu, D. Guo, J. Ye, Z. Zhan, and Z. Chen, "Image
reconstruction of compressed sensing MRI using graph-based redundant wavelet
transform," Med. Image Anal. 27
(2016) 93-104.
[17] B. M.
Dale, M. A. Brown, and R. C. Semelka, "Principles of magnetic resonance
imaging," in MRI BasicPrinciples
AndApplications, Ed: John Wiley & Sons, Ltd, (2015) 26-38.
[18] A.
Menini, G. S. Slavin, J. A. Stainsby, P. Ferry, J. Felblinger, and F. Odille,
"Motion correction of multi-contrast images applied to T1 and T2
quantification in cardiac MRI," Magn.
Reson. Mater. Phy. 28 (2015) 1-12.
[19] J.
Huang, C. Chen, and L. Axel, "Fast multi-contrast MRI
reconstruction," Magn. Reson.
Imaging 32 (2014) 1344-1352.
[20] A.
Majumdar and R. K. Ward, "Accelerating multi-echo T2 weighted MR imaging:
Analysis prior group-sparse optimization," J. Magn. Reson. 210 (2011) 90-97.
[21] H. Du
and F. Lam, "Compressed sensing MR image reconstruction using a
motion-compensated reference," Magn.
Reson Imaging. 30
(2012). 954-963.
[22] J.
Jin, F. Liu, and S. Crozier, "Image registration guided, sparsity
constrained reconstructions for dynamic MRI," Magn. Reson Imaging 32 (2014). 1403-1417.
[23] I.
Ram, M. Elad, and I. Cohen, "Redundant wavelets on graphs and high
dimensional data clouds," IEEE
Signal Proc. Let. 19 (2012) 291-294.
[24] B.
Yang and S. Li, "Pixel-level image fusion with simultaneous orthogonal
matching pursuit," Inform. Fusion 13
(2012) 10-19.
[25] F. P.
M. Oliveira and J. M. R. S. Tavares, "Medical image registration: a
review," Comput.Method. Bio-Mec. 17
(2014) 73-93.
[26] S.
Li, X. Kang, L. Fang, J. Hu, and H. Yin, "Pixel-level image fusion: a
survey of the state of the art," Inform.
Fusion, 33 (2017) 100-112.
[27] A. P.
James and B. V. Dasarathy, "Medical image fusion: a survey of the state of
the art," Inform. Fusion, 19
(2014) 4-19.
[28] H.
Ghassemian, "A review of remote sensing image fusion methods," Inform. FusionPart A 32 (2016) 75-89.
[29] L.
Tang, G. Hamarneh, and K. Iniewski, "Medical image registration: a
review," Medical Imaging: Technology
and Applications (2013) 619-660.
[30] P. J.
Kostelec and S. Periaswamy, "Image registration for MRI," Modern Signal Processing 46 (2003)
161-185.
[31] P.
Viola and W. M. Wells, "Alignment by maximization of mutual
information," In:Proceedings of the 5th international conference
on computer vision-ICCV (1995) 16-23.
[32] J. P.
W. Pluim, J. B. A. Maintz, and M. A. Viergever, "Mutual-information-based
registration of medical images: a survey," IEEE Trans. Med. Imaging 22 (2003) 986-1004.
[33] D.
Mattes, D. R. Haynor, H. Vesselle, T. K. Lewellen, and W. Eubank,
"Nonrigid multimodality image registration," SPIE, 4322 (2001) 1609-1620.
[34] M.
Styner, C. Brechbuehler, G. Székely, and G. Gerig, "Parametric estimate of
intensity inhomogeneities applied to MRI," IEEE Trans. Med. Imaging 19, (2000) 153-165.
[35] Y.
Liu, J. F. Cai, Z. Zhan, D. Guo, J. Ye, Z. Chen, and X. Qu, "Balanced
sparse model for tight frames in compressed sensing magnetic resonance
imaging," PloS One 10 (2015)
547-562.
[36] S.
Boyd, N. Parikh, E. Chu, B. Peleato, and J. Eckstein, "Distributed
optimization and statistical learning via the alternating direction method of
multipliers," Foundations and
Trends® in Machine Learning 3 (2011) 1-122.
[37] M. V.
Afonso, J. M. Bioucas-Dias, and M. A. T. Figueiredo, "Fast image recovery
using variable splitting and constrained optimization," IEEE Trans. Image Proc.19 (2010)
2345-2356.
[38] D. S.
Weller, S. Ramani, and J. A. Fessler, "Augmented lagrangian with variable
splitting for faster non-Cartesian-SPIRiT MR image reconstruction," IEEE Trans. Med. Imaging 33 (2014)
351-361.
[39] J.
Yang, Y. Zhang, and W. Yin, "A fast alternating direction method for
TVL1-L2 signal reconstruction from partial fourier data," IEEE J. Sel. Top. Signal Process. 4
(2010) 288-297.
[40] Y.
Liu, Z. Zhan, J. F. Cai, D. Guo, Z. Chen, and X. Qu, "Projected iterative
soft-thresholding algorithm for tight frames in compressed sensing magnetic
resonance imaging," IEEE Trans. Med.
Imaging 35 (2016) 2130-2140.
[41] X. Qu,
Y. Hou, F. Lam, D. Guo, J. Zhong, and Z. Chen, "Magnetic resonance image
reconstruction from undersampled measurements using a patch-based nonlocal
operator," Med. Image Anal. 18
(2014) 843-856.
[42] B.
Bilgic, V. K. Goyal, and E. Adalsteinsson, "Multi-contrast reconstruction
with Bayesian compressed sensing," Magn. Reson. Med. 66 (2011) 1601-15.
[43] B.
Bilgic and E. Adalsteinsson, "Joint Bayesian compressed sensing with prior
estimate," In:Proceedings of the 20thinternational society for
magnetic resonance in medicine – ISMRM’12 (2012) 75.
[44] W.
Zhou, A. C. Bovik, H. R. Sheikh, and E. P. Simoncelli, "Image quality
assessment: from error visibility to structural similarity," IEEE Trans. Image Proc. 13 (2004)
600-612.
[45] B.
Ning, X. Qu, D. Guo, C. Hu, and Z. Chen, "Magnetic resonance image
reconstruction using trained geometric directions in 2D redundant wavelets
domain and non-convex optimization," Magn
Reson. Imaging 31 (2013) 1611-1622.
[46] B. R,
Choi H., Neelamani R., RibeiroV., Romberg J., Guo H., et. al., "Rice
wavelet toolbox," 2009.
[47] M. H.
Kayvanrad, A. J. McLeod, J. S. H. Baxter, C. A. McKenzie, and T. M. Peters,
"Stationary wavelet transform for under-sampled MRI reconstruction," Magn. Reson Imaging 32 (2014) 1353-1364.
[48] A.
Majumdar and R. K. Ward, "Joint reconstruction of multiecho MR images
using correlated sparsity," Magn.
Reson Imaging, 29 (2011), 899-906.