基于可分离增强低秩Hankel矩阵的快速MRI重建(中文，English)

张心林¹, 鲁恒发²,郭迪³, 赖宗英⁴, 叶慧慧⁵, 彭玺⁶, 赵波⁷, 屈小波^1,*

¹ 厦门大学，电子科学系，健康医疗大数据国家研究院，生物医学智能云研发中心，中国，厦门.
² 德克萨斯大学奥斯汀分校，生物医学工程系，美国，奥斯汀.
³ 厦门理工学院，计算机与信息工程学院，中国，厦门.
⁴ 集美大学，海洋信息工程学院，中国，厦门.
⁵ 浙江大学，光学科学与工程学院，中国，杭州.
⁶ 梅奥医疗中心，放射学系，美国，罗切斯特.
⁷ 德克萨斯大学奥斯汀分校，Oden计算工程于科学学院，美国，奥斯汀.
^* Email: quxiaobo <at> xmu.edu.cn

引用

Xinlin Zhang, Hengfa Lu, Di Guo, Zongying Lai, Huihui Ye, Xi Peng, Bo Zhao, Xiaobo Qu, Accelerated MRI Reconstruction With Separable and Enhanced Low-Rank Hankel Regularization, IEEE Transactions on Medical Imaging, vol. 41, no. 9, pp.2486-98, 2022.

概要

磁共振成像是临床诊断的重要工具，但过长的采集时间一直是行业瓶颈问题之一。磁共振量化成像克服了常规磁共振成像无法定量的不足，但其一般需要多次采集，采集时间急剧增加。稀疏采样能大幅降低采样时间，但需要从欠采样数据中高保真重建图像。团队近年来另辟蹊径，从磁共振数据的采样空间（也称为k空间），将k空间建模为指数函数，并利用其低秩Hankel矩阵特性进行重建。与传统图像空间重建方法相比，采样空间重建方法具有对欠采样方式鲁棒、重建误差低、自动估计商用设备多通道相关性等优点。然而，这类方法需要构造一个巨大的块Hankel矩阵，在重建中需要相当长的计算时间和比较大的内存消耗。如何又快又好地重建磁共振图像，依然是亟待解决的问题。

本工作中，我们提出了一种二维指数函数可分离的低秩Hankel矩阵图像重建方法，可以在降低重建误差的同时，大幅缩短重建时间。所提方法成功应用在并行成像和量化成像中。实测数据实验结果表明，所提方法在并行成像和参数化成像中，和前沿的磁共振图像重建方法相比，所提方法重建误差小，具有更好的伪影抑制能力。

主要内容

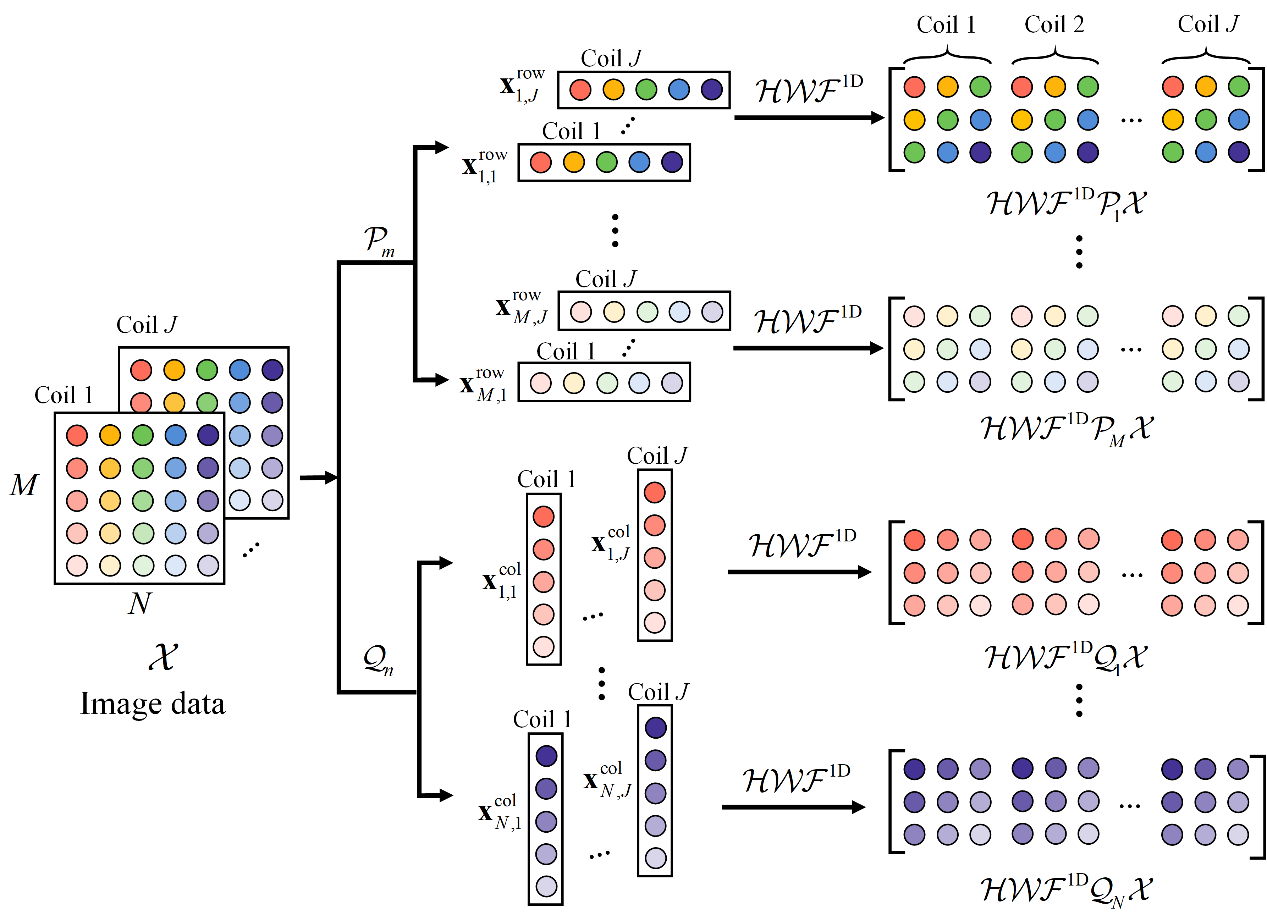
为加速重建，本工作提出将采样空间的行/列可分离地构造多个小规模Hankel矩阵（图1），这种可分离模型能显著降低计算时间（是前沿方法STDLR-SPIRiT计算时间的4%），但也忽略了行与行或列与列之间存在的相关性，导致重建误差增加。进一步，团队继续引入k空间自洽性和虚拟线圈等先验知识等更好地抑制欠采样图像伪影。在多个实测商用多通道数据表明，可分离重建模型支持灵活引入各种先验知识，在不明显增加计算量下显著提升重建图像质量，并成功实现量化成像8倍快速采集和1分钟快速重建，为肿瘤等精准快速量化成像提供了一种解决策略。

图1. 构建二维指数可分离Hankel矩阵示意图。

本工作中，我们尝试解决最先进的结构低秩方法中计算复杂度大和重建时间长的问题。为了减少计算时间，我们提出了一种可分离的Hankel低秩重建方法，称为SHLR，以增强感兴趣信号的每一行和每一列的Hankel低秩。尽管这种低秩的方法有快速运行的优势，但与块Hankel方法相比是次优的。为了提高SHLR的性能，我们引入了先验信息。对于并行成像，我们探索了行/列与虚拟线圈技术之间的相关性，并提出了SHLR-SV模型。对于参数成像，我们假设信号强度沿参数维呈指数变化。我们利用指数特性和虚拟线圈技术，提出了一种加速参数成像的SHLR-VP模型。

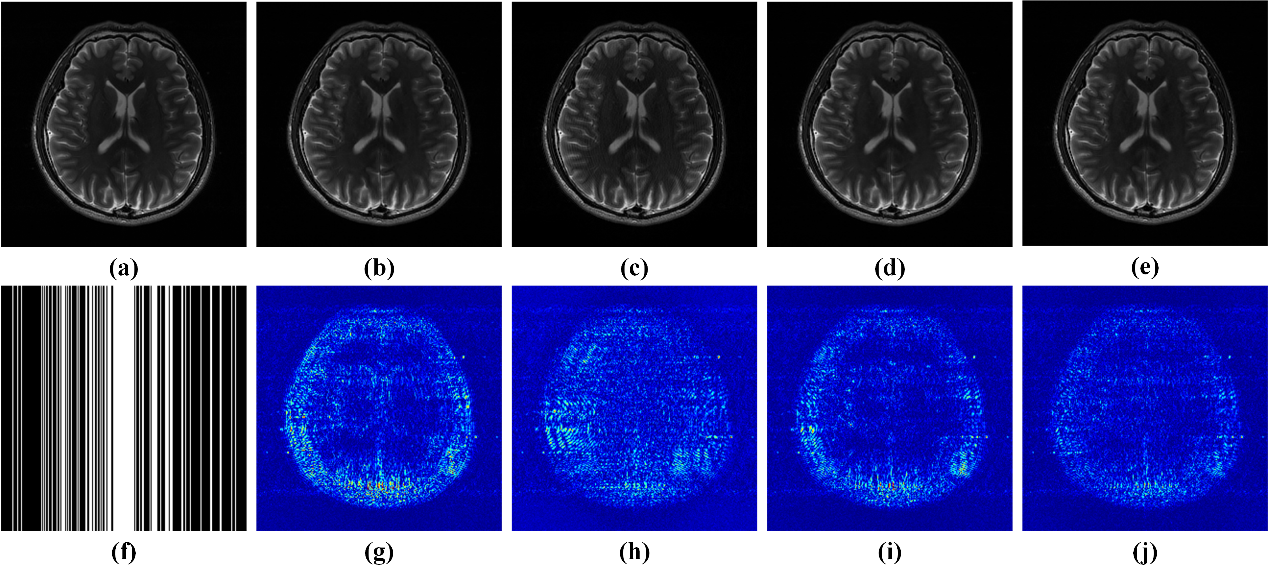
图2. 3倍加速并行成像重建结果。(a)全采样数据；(b-e)分别为L1-SPIRiT、AC-LORAKS、STDLR-SPIRiT和SHLR-VP的重建结果图；(f)3倍加速的一维随机欠采样模板；(h-j) MORASA、ALOHA和SHLR-VP在R=8处重建结果的T2 map；(g-j)上述重建图像对应的重建误差分布图(12.5×)。注：(b-e)的RLNE/MSSIM分别为0.0639/0.9873、0.0596/0.9806、0.0518/0.9918和0.0445/0.9923。

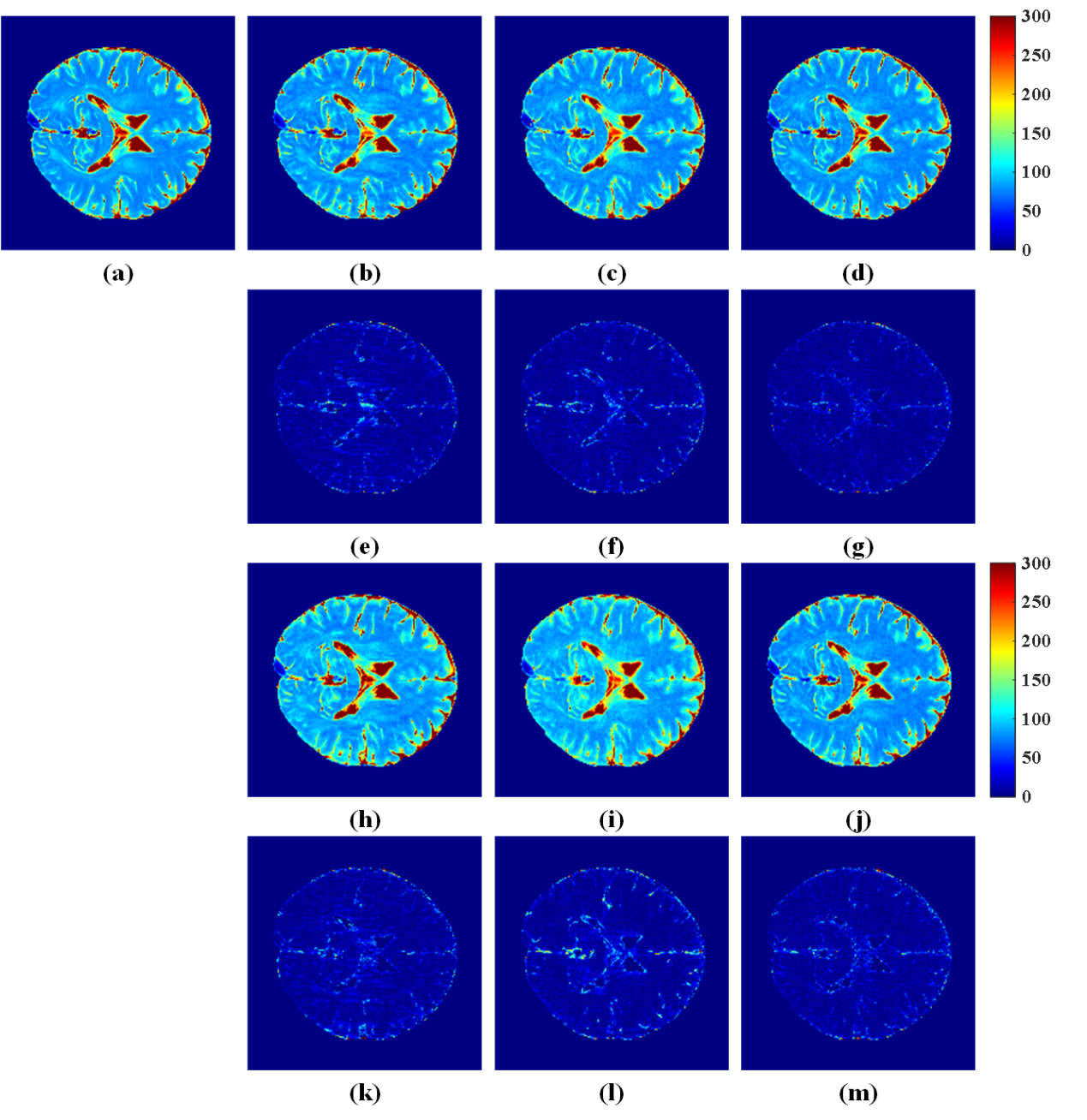
图3. 不同采样率下量化成像的重建结果。(a)全采样数据T2量化图；(b-d) 分别为MORASA、ALOHA和SHLR-VP在6倍加速下的重建T2量化图；(h-j) MORASA、ALOHA和SHLR-VP在R=8处重建结果的T2 量化图；(e-g)和(k-m)上述重建图像对应的重建误差分布图(6×)。注：(b-d)的RLNE/MSSIM分别为0.0978/0.9891、0.0959/0.9883、0.0796/0.9922，(h-j)的RLNE/MSSIM分别为0.1262/0.9831、0.1386/0.9775、0.0980/0.9880。

实测数据的实验结果表明，在并行成像和参数化成像中，和前沿的磁共振图像重建方法相比，所提方法重建误差小，具有更好的伪影抑制能力。同时，在并行成像中，所提方法重建时间是前沿方法STDLR-SPIRiT的4%；在参数化成像中，所提方法仅需64.5秒即可重建整个参数化数据，是前沿方法ALOHA的1/4。

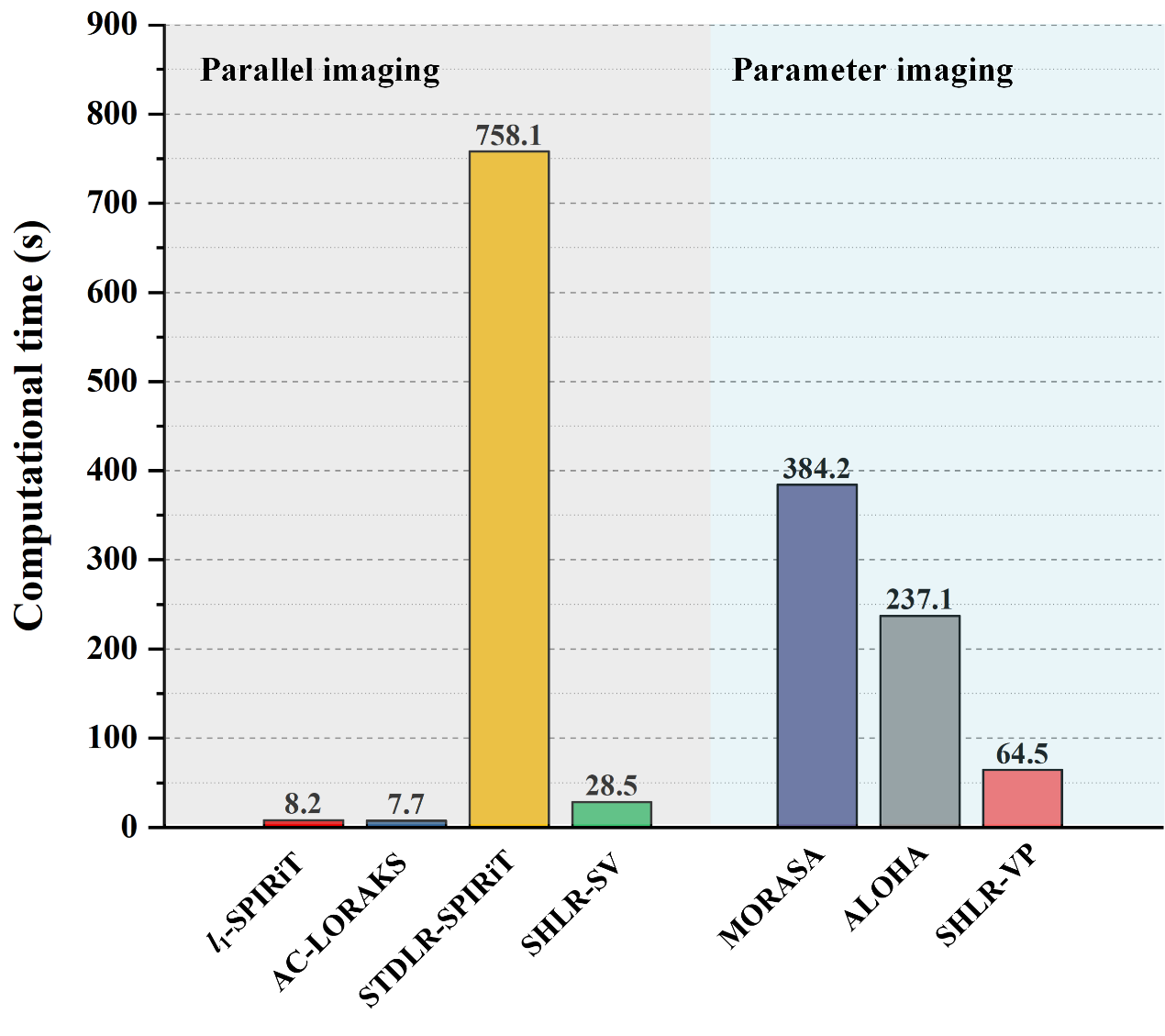
图4. 并行成像和量化成像中不同方法的计算时间。

代码下载

所提方法的MATLAB代码可以从这里下载。

致谢

这项工作得到了，国家自然科学基金（61971361、62122064、61871341和61901188），福建省自然科学基金（2021J011184），国家重点研发计划（2017YFC0108700），厦门大学南强拔尖人才计划和国家留学基金（202006310142）的资助。

参考文献

[1] J. Hamilton, D. Franson, and N. Seiberlich, “Recent advances in parallel imaging for MRI,” Progress in Nuclear Magnetic Resonance Spectroscopy, vol. 101, pp. 71–95, 2017.
[2] M. Lustig and J. M. Pauly, “SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-space,” Magnetic Resonance in Medicine, vol. 64, no. 2, pp. 457–71, 2010.
[3] J. P. Haldar, “Autocalibrated LORAKS for fast constrained MRI reconstruction,” in 2015 IEEE 12th International Symposium on Biomedical Imaging (ISBI), 2015, pp. 910–913.
[4] X. Zhang, D. Guo, Y. Huang, Y. Chen, L. Wang, F. Huang, Q. Xu, and X. Qu, “Image reconstruction with low-rankness and self-consistency of k-space data in parallel MRI,” Medical Image Analysis, vol. 63, p. 101687, 2020.
[5] X. Peng, L. Ying, Y. Liu, J. Yuan, X. Liu, and D. Liang, “Accelerated exponential parameterization of T2 relaxation with model-driven low rank and sparsity priors (MORASA),” Magnetic Resonance in Medicine, vol. 76, no. 6, pp. 1865–1878, 2016.
[6] D. Lee, K. H. Jin, E. Y. Kim, S.-H. Park, and J. C. Ye, “Acceleration of MR parameter mapping using annihilating filter-based low rank Hankel matrix (ALOHA),” Magnetic Resonance in Medicine, vol. 76, no. 6, pp. 1848–1864, 2016.