1 Department of
Electronic Science, Fujian Provincial Key Laboratory of Plasma and Magnetic
Resonance, National Institute for Data Science in Health and Medicine, Xiamen
University, Xiamen 361005, China;
2 School of Biomedical Engineering,
Shanghai Jiao Tong University, Shanghai, 200030, China;
3 United Imaging Research
Institute of Intelligent Imaging, Beijing, 100101, China;
4 Magnetic Resonance Center,
Zhongshan Hospital Xiamen University, Xiamen, 361004, China;
5 School of Computer and
Information Engineering, Xiamen University of Technology, Xiamen 361024, China.
* Correspondence: quxiaobo@xmu.edu.cn
Synopsis
Magnetic resonance
spectroscopy (MRS), as a noninvasive method for molecular structure
determination and metabolite detection, has grown into a significant tool in
clinical applications. However, the relatively low signal-to-noise ratio (SNR)
limits its further development. Although the multi-channel coil and repeated
sampling are commonly used to alleviate this problem, there is still potential
room for promotion. One possible improvement way is combining these two
acquisition methods so that the complementary of them can be well utilized. In
this paper, a novel coil combination method, average smoothing singular value
decomposition, is proposed to further improve the SNR by introducing repeatedly
sampled signals into multi-channel coil combination. Specifically, the
sensitivity matrix of each sampling is pretreated by whitened singular value
decomposition (WSVD), then the smoothing is performed along the repeated
samplings dimension. By compared with three existing popular methods, Brown,
WSVD and generalized least squares, the proposed method shows better
performance in 1 phantom and 14 in vivo spectra.
Method
1. Background
Magnetic resonance
spectroscopy (MRS), as a useful tool for determining the in vivo molecular
compositions, has achieved impressive success over the past two decades. The
main clinical application of MRS is to quantify the concentration of
metabolites, especially for the analysis of the brain neurochemistry changes
which is associated with some brain diseases like tumor[1,2],
Alzheimer's disease[3,4], Parkinson[5] and stroke[6]. However, due to the low
concentration of some metabolites and the relatively low signal-to-noise ratio
(SNR), further quantification and analysis of metabolites is difficult to be
promoted for the brain spectrum [7,8].
There are two different
conventional methods for improving the SNR of MRS. One is to average signals
obtained from the repeatedly sampled, regard as the averages di-mension (size 128 in Figure 1). The other is to receive
multi-channel spectra from phase arrays and combine them by signal processing,
regard as the coils dimension (size 32 in Figure 1). Take the sampling points
of MRS as npts dimension (size 2048 in Figure 1), then
the whole 3D MRS acquisition is shown in Figure 1. The multi-channel coil
acquisition, which is first proposed by Roemer [9] et al, simultaneously
acquires data from multiple closely overlapping magnetic resonance receiving
array in the region of interest, and has been applied in MRS and magnetic
resonance imaging [10-12]. Based on Roemer theory, several coil combination
signal processing methods have been proposed for maximizing the SNR. These
methods form a linear combination of spectra with weights (sensitivities
matrix) that provide constructive addition of the signals and give higher
emphasis to coils with higher signal[13]. An easy
evaluation of the weights is taking advantage of characteristics of the signal
itself like the amplitude of metabolite peak[14],
unsuppressed water peak[15] or the first point of its time-domain signal[15] as
the weighting coefficient. However, the above methods ignore the correlation of
the noises among coils in practice. Hence, Rodgers and Robson[16]
proposed a whitened singular value decomposition (WSVD) method aiming to reduce
the noise correlation by means of whitening before the singular value
decom-position process. Another method, named generalized least squares (GLS)
[17], which solves the inverse problem of signal recovery by using generalized
least squares, makes the coefficient of variation of the peak smaller and
provides a more reliable pretreatment for the quantification of metabolites.
Nevertheless, the improving of SNR is still not satisfying enough. One possible
promotion method is utilizing the information of two acquisition ways
simultaneously.
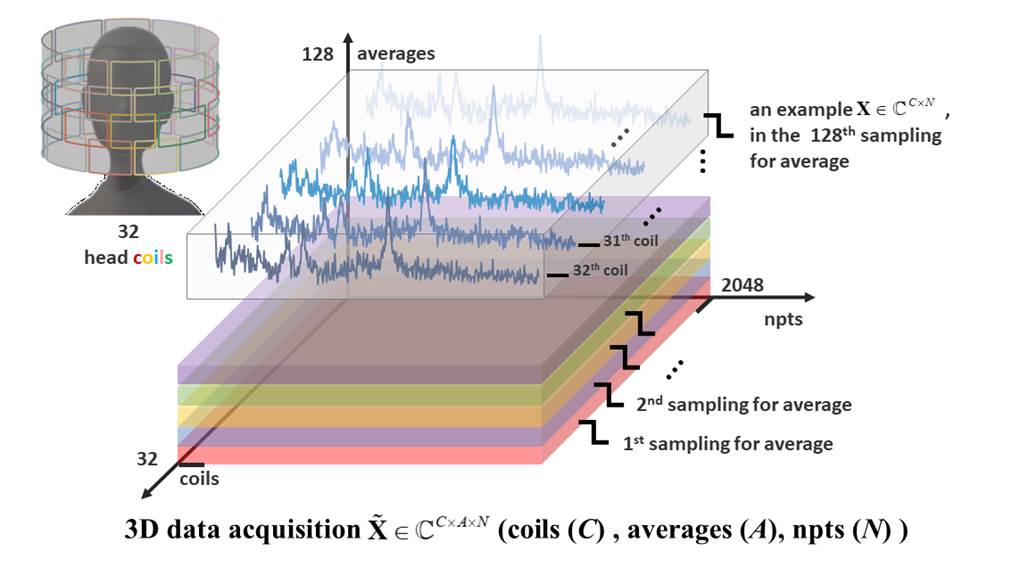
Figure 1. An illustration of the
array coil acquisition with repeatedly sampled.
2. Method
Based on the WSVD which de-correlates the noise
by signal whitening, we pro-posed a multi-coil channel combination method with
the repeated samplings, ASSVD, which extracts the information among the
repeated samplings through the convolution to gain a higher SNR. The advantages
of WSVD are absorbed into the proposed method. In the meanwhile, ASSVD takes
the relationship between repeated samplings into the consideration, making the
sensitivity matrix between each repeated sampling smoother. The more details of
model and its solution process are described in the paper.
3. Main result
Coil-combined
in vivo spectra with four methods (Brown, WSVD, GLS and proposed ASSVD)
and the fitting residuals by LCModel are shown in Figure 2, verifying that
ASSVD had a supreme SNR improvement compared with Brown and WSVD, from 40 dB to
44 dB. Besides, in the 1.4-2.0 ppm segments, the
proposed ASSVD obviously reduced noises compared with other methods, and in the
2.8-3.0 ppm and 0.4-0.6 ppm segments, the resultant spectrum also has less
noise. This promotion is benefited from that ASSVD not only took advantage of
the multi-coil acquisition but also integrated the information between repeated
samplings for maximizing the SNR. Therefore, ASSVD is expectedly suitable for
MRS which is acquired with repeated samplings in routines and has a great
application prospect.
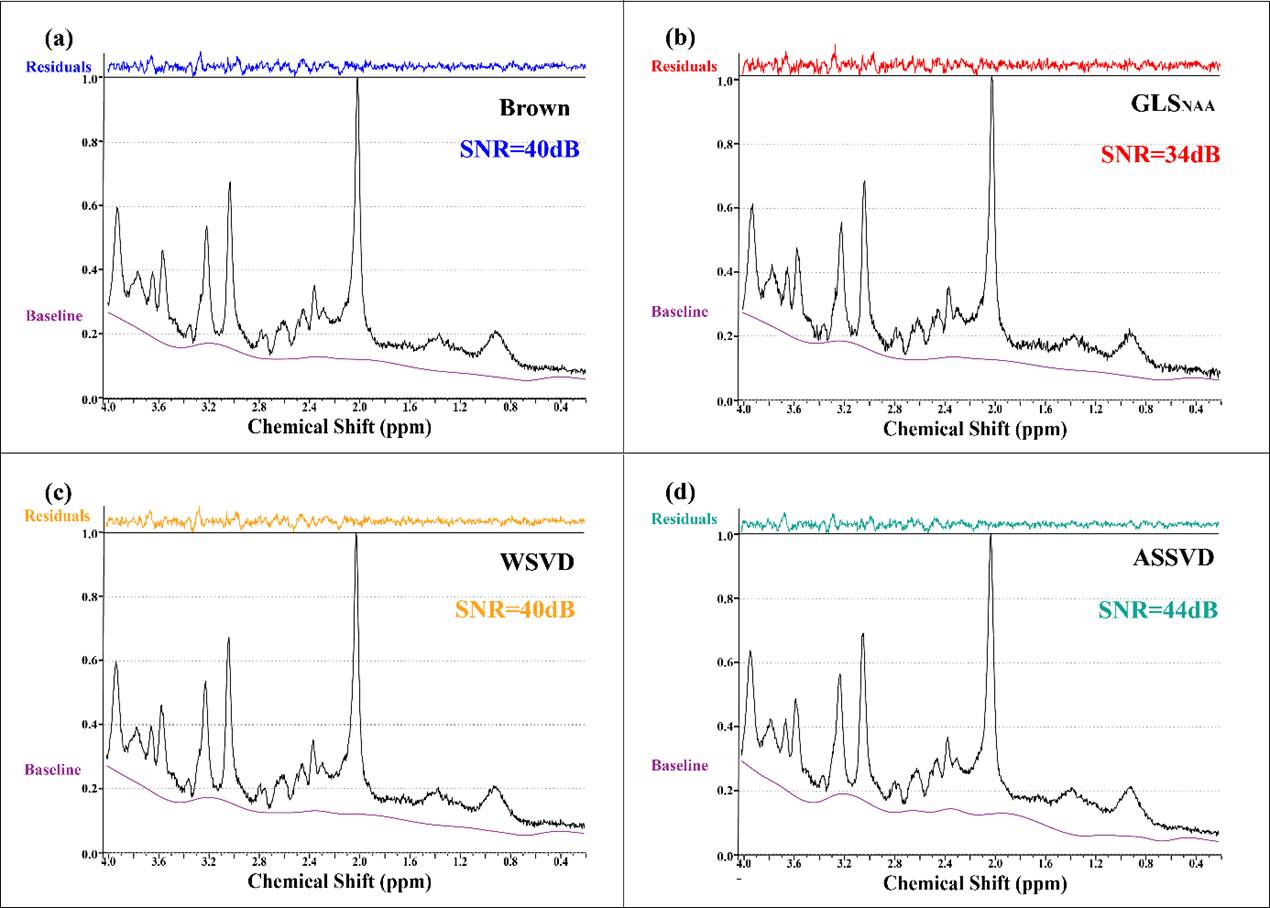
Figure
2. In vivo MRS coil-combined results. (a) Brown,
(b) GLS using NAA peak as the reference, (c) WSVD and (d) the proposed method
ASSVD. The black and purple lines represent coil-combined MRS ![]() and the baseline
and the baseline ![]() estimated by
LCModel [18] respectively. Besides, the residuals shown at the top is
calculated by
estimated by
LCModel [18] respectively. Besides, the residuals shown at the top is
calculated by ![]() where
where ![]() is for the fitting of LCModel.
is for the fitting of LCModel.
Code
The MATLAB code of ASSVD-toolbox can be
downloaded here.
Acknowledgments
This work was supported in part by National
Natural Science Foundation of China (61971361, 61871341, 61811530021 and
61672335), National Key R&D Program of China (2017YFC0108703),
Health-Education Joint Research Project of Fujian Province (2019-WJ-31), Xiamen
University Nanqiang Outstanding Talents Program. The
authors would like to thank the staff from Shanghai Jiao Tong University and
Zhongshan Hospital Xiamen University for technical support.
References:
[1]
Brandão, L.A.; Castillo, M. Adult brain tumors: Clinical applications of
magnetic resonance spectroscopy. Neuroimaging Clinics 2013, 23, 527-555;
[2] Lukas, L.; Devos, A.; Suykens, J.A.; Vanhamme, L.; Howe, F.A.; Majós, C.; Moreno-Torres, A.; Van der Graaf, M.; Tate,
A.R.; Arús, C. Brain tumor classification based on
long echo proton MRS signals. Artificial Intelligence in Medicine 2004, 31,
73-89;
[3] Gao, F.; Barker, P.B. Various MRS
application tools for Alzheimer disease and mild cognitive impairment. American
Journal of Neuroradiology 2014, 35, S4-S11;
[4] Pardon, M.-C.; Lopez, M.Y.; Yuchun, D.; Marjańska, M.; Prior,
M.; Brignell, C.; Parhizkar, S.; Agostini, A.; Bai,
L.; Auer, D.P. Magnetic resonance spectroscopy discriminates the response to
microglial stimulation of wild type and Alzheimer’s disease models. Scientific
Reports 2016, 6, 1-12;
[5] Sian, J.; Dexter,
D.T.; Lees, A.J.; Daniel, S.; Agid, Y.; Javoy, F.; Jenner, P.; Marsden, C.D. Alterations in
glutathione levels in Parkinson's disease and other neurodegenerative disorders
affecting basal ganglia. Annals of Neurology 1994, 36, 348-355.
[6] Saunders, D.E. MR spectroscopy in
stroke. British Medical Bulletin 2000, 56, 334-345;
[7] Poullet,
J.-B.; Sima, D.M.; Van Huffel, S. MRS signal
quantitation: A review of time-and frequency-domain methods. Journal of
Magnetic Resonance 2008, 195, 134-144;
[8] Provencher, S.W.
Estimation of metabolite concentrations from localized in vivo proton NMR
spectra. Magnetic Resonance in Medicine 1993, 30, 672-679;
[9] Roemer, P.B.; Edelstein, W.A.;
Hayes, C.E.; Souza, S.P.; Mueller, O.M. The NMR phased array. Magnetic
Resonance in Medicine 1990, 16, 192-225;
[10] Pruessmann, K.P.; Weiger, M.; Scheidegger, M.B.; Boesiger,
P. SENSE: Sensitivity encoding for fast MRI. Magnetic Resonance in Medicine
1999, 42, 952-962;
[11] Zhang, X.; Lu,
H.; Guo, D.; Bao, L.; Huang, F.; Xu, Q.; Qu, X. A guaranteed convergence
analysis for the projected fast iterative soft-thresholding algorithm in
parallel MRI. Medical Image Analysis 2021, 69, 101987;
[12] Hu, Y.; Zhang,
X.; Feng, L.; Chen, D.; Yan, Z.; Shen, X.; Yan, G.; Ou-yang,
L.; Qu, X. Spatiotemporal Flexible Sparse Reconstruction for Rapid Dynamic
Contrast-enhanced MRI. arXiv preprint
arXiv:2007.02937 2020;
[13] Vareth, M.; Lupo, J.M.; Larson, P.E.; Nelson, S.J. A comparison of
coil combination strategies in 3D multi-channel MRSI reconstruction for
patients with brain tumors. NMR in Biomedicine 2018, 31, e3929;
[14] Hardy, C.J.;
Bottomley, P.A.; Rohling, K.W.; Roemer, P.B. An NMR phased array for human
cardiac 31P spectroscopy. Magnetic Resonance in Medicine 1992, 28, 54-64;
[15] Brown, M.A.
Time-domain combination of MR spectroscopy data acquired using phased-array
coils. Magnetic Resonance in Medicine 2004, 52, 1207-1213;
[16] Rodgers, C.T.;
Robson, M.D. Receive array magnetic resonance spectroscopy: Whitened singular
value decomposition (WSVD) gives optimal Bayesian solution. Magnetic Resonance
in Medicine 2010, 63, 881-891;
[17] An, L.; Willem
van der Veen, J.; Li, S.; Thomasson, D.M.; Shen, J. Combination of multichannel
single-voxel MRS signals using generalized least squares. Journal of Magnetic
Resonance Imaging 2013, 37, 1445-1450.
[18] Provencher, S.W.
Automatic quantitation of localized in vivo 1H spectra with LCModel. NMR in
Biomedicine 2001, 14, 260-264.