Convex Dual Theory Analysis of Two-Layer Convolutional Neural Networks with Soft-Thresholding(中文,English)
Chunyan Xiong1,
Chaoxing Zhang2,
1Institute of Electromagnetics and Acoustics, Fujian Provincial Key Laboratory of Plasma and Magnetic Resonance, Xiamen University, Xiamen, China.
2Department of electronic science, Fujian Provincial Key Laboratory of Plasma and Magnetic Resonance, Biomedical Intelligent Cloud Research and Development Center, Xiamen University, Xiamen, China.
3 The School of Computer and Information Engineering, Xiamen University of Technology, Xiamen, China.
* Email: quxiaobo <at> xmu.edu.cn
Citation
Chunyan Xiong, Chaoxing Zhang, Mengli Lu, Xiaotong Yu, Jian Cao, Zhong Chen, Di Guo, and Xiaobo Qu, Convex Dual Theory Analysis of Two-Layer Convolutional Neural Networks with Soft-Thresholding, IEEE Transactions on Neural Networks and Learning Systems, DOI: 10.1109/TNNLS.2024.3353795
Synopsis
Soft-thresholding has been widely used in neural networks. Its basic network structure is a two-layer convolution neural network with soft-thresholding. Due to the network’s nature of nonlinear and non-convex, the training process heavily depends on an appropriate initialization of network parameters, resulting in the difficulty of obtaining a globally optimal solution, which poses challenges in pixel-sensitive fields such as medical imaging and so on.
To address this issue, a convex dual network is designed here. We theoretically analyze the network convexity and prove that the strong duality holds. Extensive results on both simulation and real-world datasets show that strong duality holds, the dual network does not depend on initialization and optimizer, and enables faster convergence than the state-of-the-art two layer network. This work provides a new way to convexify soft-thresholding neural networks. Furthermore, the convex dual network model of a deep soft-thresholding network with a parallel structure is deduced.
Main Context
To solve the problem that the primal soft-thresholding network model is non-convex and the optimal solution depends on the initialization method and the selection of optimizer, a convex dual network model(Fig.1) is designed in this paper. Firstly, the weak dual model is derived by using Lagrange's theorem, Then, in order to provide a more accurate representation of the network training process. Next, based on the characteristics of the soft-thresholding, this paper constructs a diagonal matrix, transforms the nonlinear operation into a linear operation without changing the objective value, and divides the hyperplane(Fig.2). Finally, the strong dual is proved to be valid by combining the convex optimization theory. Real-world datasets show that strong duality holds(Fig.3), the dual network does not depend on initialization (Fig.4) and optimizer(Fig.5).

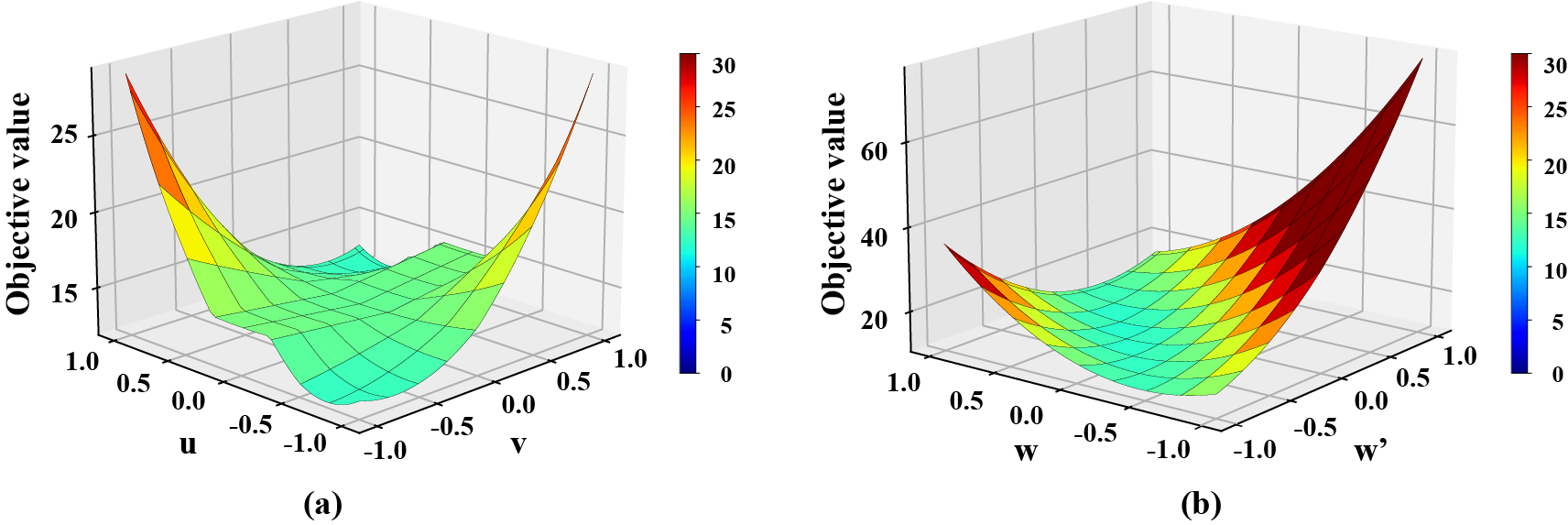
Fig. 2. Objective value of a two-layer primal ST-CNN and dual ST-CNN trained with ADAM on a one-dimensional dataset. Assuming $x = [−1, 2, 0, 1, 2]^{⊤}$ and $y = [2, 1, 2, 1, 2]^{⊤}$, which are the input and output, respectively. (a) Non-convex primal ST-CNN, (b) convex dual ST-CNN.
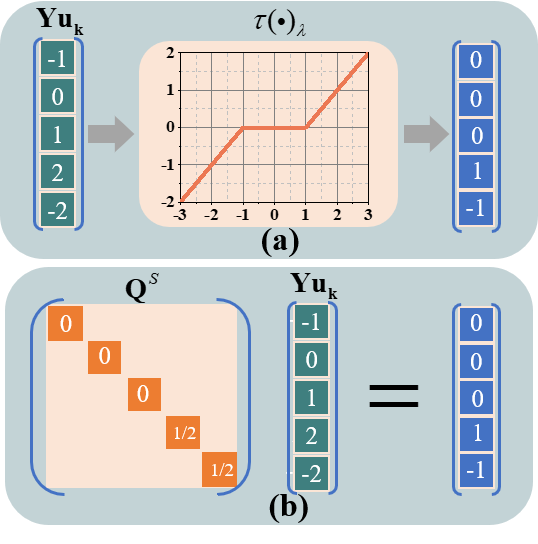
Fig. 2. Toy example: Converting non-linear operation to linear operation. (a) Soft-thresholding in the primal neural network, (b) diagonal matrix in the dual neural network.
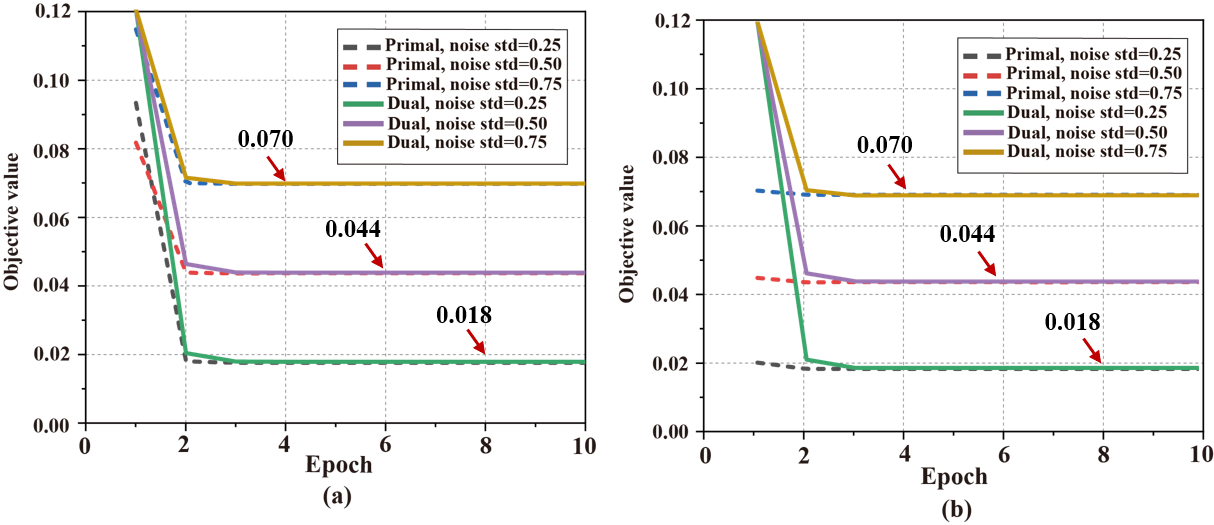
Fig. 3. Verification of the zero dual gap (the strong duality), i.e. the objective values are very close when both the primal and dual networks achieve the global optimality. (a) and (b) is the objective value under the training and test stage (networks are trained), respectively. Note: Noise is added following a Gaussian distribution with the mean 0 and the standard deviations 0.25, 0.50, and 0.75, respectively.
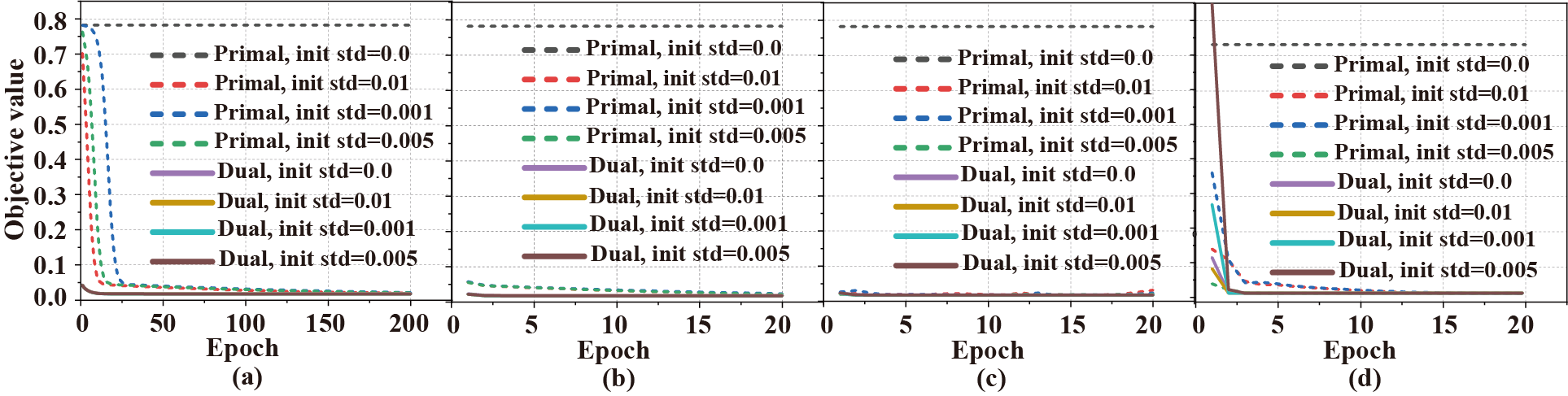
Fig. 4. The objective value of the primal and dual network under different optimizers and different initialization modes. (a)-(d) are results under the optimizer of Stochastic Gradient Descent with Momentum, AdaGrad, RMSProp, and Adam, respectively.
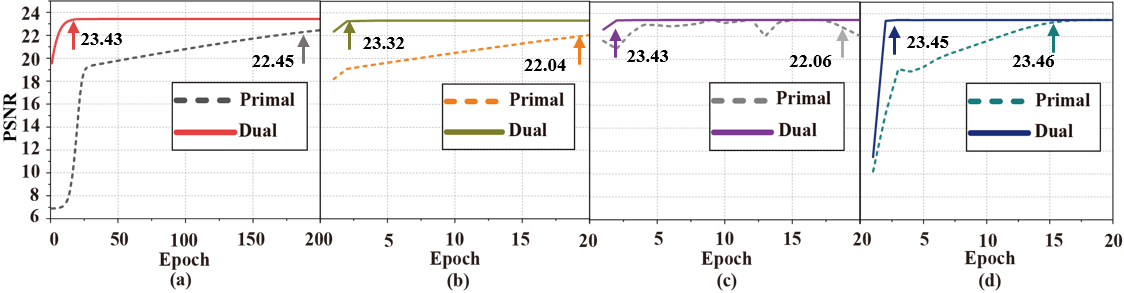
Fig. 14. PSNR performance of the primal and dual networks under different optimizers. (a)-(d) are results under the optimizer of Stochastic Gradient Descent with Momentum, AdaGrad, RMSProp, and Adam, respectively. Note: The PSNR is averaged on 400 noisy images after the networks have been trained. All network parameters are initialized following a normal distribution $N(0,0.001^{2})$.
Code
The python code of this work can be downloaded here.
Acknowledgements
This work was supported in part by the National Natural Science Foundation of China under Grant 61971361, Grant 62122064, Grant 62331021, and Grant 62371410; in part by the Natural Science Foundation of Fujian Province of China under Grant 2023J02005 and Grant 2021J011184; President Fund of Xiamen University (20720220063); in part by the Xiamen University Nanqiang Outstanding Talents Program.
References
[1] J. Hamilton, D. Franson, and N. Seiberlich, “Recent advances in parallel imaging for MRI,” Progress in Nuclear Magnetic Resonance Spectroscopy, vol. 101, pp. 71–95, 2017.
[2] M. Lustig and J. M. Pauly, “SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-space,” Magnetic Resonance in Medicine, vol. 64, no. 2, pp. 457–71, 2010.
[3] J. P. Haldar, “Autocalibrated LORAKS for fast constrained MRI reconstruction,” in 2015 IEEE 12th International Symposium on Biomedical Imaging (ISBI), 2015, pp. 910–913.
[4] X. Zhang, D. Guo, Y. Huang, Y. Chen, L. Wang, F. Huang, Q. Xu, and X. Qu, “Image reconstruction with low-rankness and self-consistency of k-space data in parallel MRI,” Medical Image Analysis, vol. 63, p. 101687, 2020.
[5] X. Peng, L. Ying, Y. Liu, J. Yuan, X. Liu, and D. Liang, “Accelerated exponential parameterization of T2 relaxation with model-driven low rank and sparsity priors (MORASA),” Magnetic Resonance in Medicine, vol. 76, no. 6, pp. 1865–1878, 2016.
[6] D. Lee, K. H. Jin, E. Y. Kim, S.-H. Park, and J. C. Ye, “Acceleration of MR parameter mapping using annihilating filter-based low rank Hankel matrix (ALOHA),” Magnetic Resonance in Medicine, vol. 76, no. 6, pp. 1848–1864, 2016.