pFISTA-SENSE-ResNet for Parallel MRI Reconstruction ( [Chinese] )
Tieyuan Lu1, Xinlin Zhang1, Yihui Huang1, Di Guo2, Feng Huang3, Qin Xu3, Yuhan Hu1, Lin Ou-Yang4,5, Jianzhong Lin6, Zhiping Yan
7, Xiaobo Qu1**
1Department of Electronic Science, Fujian Provincial Key Laboratory of Plasma and Magnetic Resonance, School of Electronic Science and Engineering, Xiamen University, Xiamen 361005, China.
2School of Computer and Information Engineering, Fujian Provincial University Key Laboratory of Internet of Things Application Technology, Xiamen University of Technology, Xiamen 361024, China.
3Neusoft Medical System, Shanghai 200241, China.;
4Department of Medical Imaging of Southeast Hospital, Medical College of Xiamen University, Zhangzhou 363000, China..
5Institute of Medical Imaging of Medical College of Xiamen University, Zhangzhou 363000, China.;
6Magnetic Resonance Center, Zhongshan Hospital Xiamen University, Xiamen 361004, China..
7Department of Radiology, Fujian Medical University Xiamen Humanity Hospital, Xiamen 361000, China..
Concat:
quxiaobo<|at|>xmu.edu.cn
Citation: Tieyuan Lu, Xinlin Zhang, Yihui Huang, Di Guo, Feng Huang, Qin Xu, Yuhan Hu, Lin Ou-Yang, Jianzhong Lin, Zhiping Yan, Xiaobo Qu*, pFISTA-SENSE-ResNet for Parallel MRI Reconstruction,Journal of Magnetic Resonance, DOI: 10.1016/j.jmr.2020.106790, 2020.
Access to full text:https://authors.elsevier.com/a/1bW4K3u0yjN8GV
Abstract:
Magnetic resonance imaging(MRI)has been widely applied in clinical diagnosis. However, it is limited by its long data acquisition time. Although the imaging can be accelerated by sparse sampling and parallel imaging, achieving promising reconstructed images with a fast computation speed remains a challenge. Recently, deep learning methods have attracted a lot of attention for encouraging reconstruction results, but they are lack of proper interpretability for neural networks. In this work, in order to enable high-quality image reconstruction for the parallel magnetic resonance imaging, we design the network structure from the perspective of sparse iterative reconstruction and enhance it with the residual structure. Experimental results on a public knee dataset indicate that, as compared with the state-of-the-art deep learning-based and optimization-based methods, the proposed network achieves lower error in reconstruction and is more robust under different samplings.
KEYWORDS:
Magnetic resonance imaging, image reconstruction, deep learning, sparse learning, network interpretability.
Methods:
1.
Background
As key problems in MRI reconstruction, better image quality and faster reconstruction are still great challenges and worthy of investigation. To achieve a lower reconstruction error with compressed sensing (CS) methods, several data-free sparse transforms, including the fixed ones and the adaptive ones have been used. Recently, the database-based deep learning method has been applied in many applications, including biological magnetic resonance spectroscopy, medical image analysis, and accelerating MRI image reconstruction, and obtained outstanding performances with the powerful deep convolution neural network (CNN). However, comparing with optimization-based iterative algorithms, CNN appears to be a black box in the image reconstruction process.
To improve the interpretability, some optimization-based algorithms have been unrolled and yielded as deep learning networks, such as: VN and MoDL. However, the single convolution layer used as the regular term in VN limits the reconstruction quality. MoDL incorporates the conjugate gradient optimization into the network to solve the data consistency subproblem which slows down the reconstruction speed.
2.
pFISTA-SENSE-ResNet
We unroll the iteration of pFISTA-SENSE as the basic structure of our proposed network, and the  iteration block can be written as:
iteration block can be written as:


where is the sensitivity map of the
is the sensitivity map of the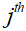 coil,
coil,  is the Fourier transform,
is the Fourier transform,  is the undersampling matrix,
is the undersampling matrix, is the acquired k-space data of the
is the acquired k-space data of the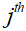 coil,
coil,  is the step size,
is the step size, and
and denote conjugate transpose and transpose respectively,
denote conjugate transpose and transpose respectively,  is a pointwise soft-thresholding function,
is a pointwise soft-thresholding function,  .
. and
and  are the forward operation and the backward operation, both of which are made up of CNN blocks.
are the forward operation and the backward operation, both of which are made up of CNN blocks.
The structure of the proposed network is shown in Figure 1.

 iteration block in (a).
iteration block in (a).3.
Main Results
he proposed method is compared with data-free pFISTA-SENSE and two data-based deep learning methods: VN and MoDL. Figure 2 shows the reconstruction result of a public knee dataset under acceleration factor of 7. Image recovered by pFISTA-SENSE-ResNet is closer to the fully sampled images than others. First, the result of pFISTA-SENSE-ResNet (Figure 2(e)) is less blurred than pFISTA-SENSE (Figure 2(b)), and the undersampling artifacts are well suppressed compared with MoDL (Figure 2(d)), as the yellow arrow pointing in Figure 2(d). Second, small details are recovered more faithfully than other methods, such as the red arrows pointing in Figure 2. Besides, less error is observed at the reconstruction results of pFISTA-SENSE-ResNet according to the error maps.

Acknowledgments:
This work was supported in part by National Key R&D Program of China (2017YFC0108703), National Natural Science Foundation of China (61971361, 61871341, and 61811530021), Natural Science Foundation of Fujian Province of China (2018J06018), Fundamental Research Funds for the Central Universities (20720180056), and Xiamen University Nanqiang Outstanding Talents Programme. The authors would like thank the GPU donated by NVIDIA Corporation. The authors would like thank Yonggui Yang, Gang Guo of the Department of Radiology of the Second Affiliated Hospital of Xiamen Medical College, and Lijun Bao of Department of Electronic Science of Xiamen University for revising the paper. The authors would like thank to the reviewers for their valuable suggestions on this paper.
Reference:
[1] M. Lustig, D. Donoho, and J. M. Pauly, "Sparse MRI: The application of compressed sensing for rapid MR imaging," Magnetic Resonance in Medicine, vol. 58, no. 6, pp. 1182-1195, 2007.
[2] J. Hamilton, D. Franson, and N. Seiberlich, "Recent advances in parallel imaging for MRI," Progress in Nuclear Magnetic Resonance Spectroscopy, vol. 101, pp. 71-95, 2017.
[3] Z.-P. Liang, "Spatiotemporal imaging with partially separable functions," in 2007 4th IEEE International Symposium on Biomedical Imaging: From Nano to Macro, 2007, pp. 988-991.
[4] X. Qu, Y. Hou, F. Lam, D. Guo, J. Zhong, and Z. Chen, "Magnetic resonance image reconstruction from undersampled measurements using a patch-based nonlocal operator," Medical Image Analysis, vol. 18, no. 6, pp. 843-856, 2014.
[5] K. P. Pruessmann, M. Weiger, M. B. Scheidegger, and P. Boesiger, "SENSE: Sensitivity encoding for fast MRI," Magnetic Resonance in Medicine, vol. 42, no. 5, pp. 952-962, 1999.
[6] J. Jin, F. Liu, E. Weber, Y. Li, and S. Crozier, "An electromagnetic reverse method of coil sensitivity mapping for parallel MRI鈥揟heoretical framework," Journal of Magnetic Resonance, vol. 207, no. 1, pp. 59-68, 2010.
[7] B. Liu, F. Sebert, Y. Zou, and L. Ying, "SparseSENSE: Randomly-sampled parallel imaging using compressed sensing," in 16th Annual Meeting of ISMRM, 2008, p. 3154.
[8] D. Liang, B. Liu, J. Wang, and L. Ying, "Accelerating SENSE using compressed sensing," Magnetic Resonance in Medicine, vol. 62, no. 6, pp. 1574-1584, 2009.
[9] X. Qu, W. Zhang, D. Guo, C. Cai, S. Cai, and Z. Chen, "Iterative thresholding compressed sensing MRI based on contourlet transform," Inverse Problems in Science and Engineering, vol. 18, no. 6, pp. 737-758, 2010.
[10] S. Pejoski, V. Kafedziski, and D. Gleich, "Compressed sensing MRI using discrete nonseparable shearlet transform and FISTA," IEEE Signal Processing Letters, vol. 22, no. 10, pp. 1566-1570, 2015.
[11] X. Qu et al., "Undersampled MRI reconstruction with patch-based directional wavelets," Magnetic Resonance Imaging, vol. 30, no. 7, pp. 964-977, 2012.
[12] S. Ravishankar and Y. Bresler, "MR image reconstruction from highly undersampled k-space data by dictionary learning," IEEE Transactions on Medical Imaging, vol. 30, no. 5, pp. 1028-1041, 2010.
[13] Z. Lai et al., "Image reconstruction of compressed sensing MRI using graph-based redundant wavelet transform," Medical Image Analysis, vol. 27, pp. 93-104, 2016.
[14] Z. Zhan, J.-F. Cai, D. Guo, Y. Liu, Z. Chen, and X. Qu, "Fast multiclass dictionaries learning with geometrical directions in MRI reconstruction," IEEE Transactions on Biomedical Engineering, vol. 63, no. 9, pp. 1850-1861, 2015.
[15] X. Qu et al., "Accelerated nuclear magnetic resonance spectroscopy with deep learning," Angewandte Chemie International Edition, vol. 59, no. 26, pp. 10297-10300, 2020.
[16] D. Chen, Z. Wang, D. Guo, V. Orekhov, and X. Qu, "Review and prospect: Deep learning in nuclear magnetic resonance spectroscopy," Chemistry-A European Journal, 2020. DOI: 10.1002/chem.202000246.
[17] W. Lin et al., "Convolutional neural networks-based MRI image analysis for the alzheimer鈥檚 disease prediction from mild cognitive impairment," Frontiers in Neuroscience, vol. 12, p. 777, 2018.
[18] S. Wang et al., "Accelerating magnetic resonance imaging via deep learning," in IEEE International Symposium on Biomedical Imaging, 2016, pp. 514-517.
[19] J. Zhang et al., "Robust single-shot T 2 mapping via multiple overlapping-echo acquisition and deep neural network," IEEE Transactions on Medical Imaging, vol. 38, no. 8, pp. 1801-1811, 2019.
[20] L. Bao et al., "Undersampled MR image reconstruction using an enhanced recursive residual network," Journal of Magnetic Resonance, vol. 305, pp. 232-246, 2019.
[21] J. Schlemper, J. Caballero, J. V. Hajnal, A. N. Price, and D. Rueckert, "A deep cascade of convolutional neural networks for dynamic MR image reconstruction," IEEE Transactions on Medical Imaging, vol. 37, no. 2, pp. 491-503, 2018.
[22] K. Zeng, Y. Yang, G. Xiao, and Z. Chen, "A very deep densely connected network for compressed sensing MRI," IEEE Access, vol. 7, pp. 85430-85439, 2019.
[23] Y. Yang, J. Sun, H. Li, and Z. Xu, "Deep ADMM-Net for compressive sensing MRI," in Advances in Neural Information Processing Systems, 2016, pp. 10-18.
[24] J. Zhang and B. Ghanem, "ISTA-Net: Interpretable optimization-inspired deep network for image compressive sensing," in IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 1828-1837.
[25] J. Cheng, H. Wang, Y. Zhu, Q. Liu, L. Ying, and D. Liang, "Model-based deep MR imaging: The roadmap of generalizing compressed sensing model using deep learning," arXiv preprint arXiv:1906.08143, 2019.
[26] K. Hammernik et al., "Learning a variational network for reconstruction of accelerated MRI data," Magnetic Resonance in Medicine, vol. 79, no. 6, pp. 3055-3071, 2017.
[27] L. Landweber, "An iteration formula for Fredholm integral equations of the first kind," American Journal of Mathematics, vol. 73, no. 3, pp. 615-624, 1951.
[28] H. K. Aggarwal, M. P. Mani, and M. Jacob, "MoDL: Model based deep learning architecture for inverse problems," IEEE Transactions on Medical Imaging, vol. 38, no. 2, pp. 394-405, 2018.
[29] Y. Liu, Z. Zhan, J. Cai, D. Guo, Z. Chen, and X. Qu, "Projected iterative soft-thresholding algorithm for tight frames in compressed sensing magnetic resonance imaging," IEEE Transactions on Medical Imaging, vol. 35, no. 9, pp. 2130-2140, 2016.
[30] I. Daubechies, M. Defrise, and C. De Mol, "An iterative thresholding algorithm for linear inverse problems with a sparsity constraint," Communications on Pure and Applied Mathematics, vol. 57, no. 11, pp. 1413-1457, 2004.
[31] A. Beck and M. Teboulle, "A fast iterative shrinkage-thresholding algorithm for linear inverse problems," SIAM Journal on Imaging Sciences, vol. 2, no. 1, pp. 183-202, 2009.
[32] Y. Liu et al., "Balanced sparse model for tight frames in compressed sensing magnetic resonance imaging," PLoS One, vol. 10, no. 4, p. e0119584, 2015.
[33] S. T. Ting et al., "Fast implementation for compressive recovery of highly accelerated cardiac cine MRI using the balanced sparse model," Magnetic Resonance in Medicine, vol. 77, no. 4, pp. 1505-1515, 2017.
[34] X. Zhang, H. Lu, D. Guo, L. Bao, F. Huang, and X. Qu, "A convergence proof of projected fast iterative soft-thresholding algorithm for parallel magnetic resonance imaging," arXiv preprint arXiv:1909.07600, 2019.
[35] V. Nair and G. E. Hinton, "Rectified linear units improve restricted boltzmann machines," in 27th International Conference on Machine Learning, 2010, pp. 807-814.
[36] K. He, X. Zhang, S. Ren, and J. Sun, "Deep residual learning for image recognition," in IEEE Conference on Computer Vision and Pattern Recognition, 2016, pp. 770-778.
[37] M. Uecker et al., "ESPIRiT鈥攁n eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA," Magnetic Resonance in Medicine, vol. 71, no. 3, pp. 990-1001, 2014.
[38] X. Glorot and Y. Bengio, "Understanding the difficulty of training deep feedforward neural networks," in Proceedings of the 13th International Conference on Artificial Intelligence and Statistics, 2010, pp. 249-256.
[39] D. P. Kingma and J. Ba, "Adam: A method for stochastic optimization," arXiv preprint arXiv:1412.6980, 2014.
[40] Z. Wang, A. C. Bovik, H. R. Sheikh, and E. P. Simoncelli, "Image quality assessment: From error visibility to structural similarity," IEEE Transactions on Image Processing, vol. 13, no. 4, pp. 600-612, 2004.
[41] D. Narnhofer, K. Hammernik, F. Knoll, and T. Pock, "Inverse GANs for accelerated MRI reconstruction," in Wavelets and Sparsity XVIII, 2019.
[42] Y. Han, J. Yoo, H. H. Kim, H. J. Shin, and J. C. Ye, "Deep learning with domain adaptation for accelerated projection-reconstruction MR," Magnetic Resonance in Medicine, vol. 80, no. 3, pp. 1189-1205, 2018.