Phase-Constrained Reconstruction of High-Resolution Multi-shot
Diffusion Weighted Image ( [Chinese] )
Yiman Huang1,
Xinlin Zhang1, Hua Guo2, Huijun Chen2, Di Guo3,
Feng Huang4, Qin Xu4, Xiaobo Qu1*
1Department of Electronic Science, Fujian Provincial Key Laboratory
of Plasma and Magnetic Resonance, School of Electronic Science and Engineering,
Xiamen University, Xiamen 361005, China.
2Center for Biomedical Imaging Research, Department of Biomedical
Engineering, Tsinghua University, Beijing, 100084, China.
3School of Computer and Information Engineering, Fujian Provincial
University Key Laboratory of Internet of Things Application Technology, Xiamen
University of Technology, Xiamen 361024, China.
4Neusoft Medical System, Shanghai 200241, China.
Contact:
quxiaobo<|at|>xmu.edu.cn
Citations: Yiman Huang, Xinlin Zhang, Hua Guo,
Huijun Chen, Di Guo, Feng Huang, Qin Xu, Xiaobo Qu*, Phase-constrained
reconstruction of high-resolution multi-shot diffusion weighted magnetic
resonance image, Journal of Magnetic Resonance, DOI: 10.1016/j.jmr.2020.106690,
2020.
Access
to full text:https://authors.elsevier.com/a/1aZ%7EG3u0yjN80o
Abstract:
Diffusion weighted imaging (DWI) is
a unique examining method in tumor diagnosis, acute stroke evaluation.
Single-shot echo planar imaging is currently conventional method for DWI.
However, single-shot DWI suffers from image distortion, blurring and low
spatial resolution. Although multi-shot DWI improves image resolution, it
brings phase variations among different shots at the same time. We introduce a
smooth phase constraint of each shot image into multi-shot navigator-free DWI
reconstruction by imposing the low-rankness of Hankel matrix constructed from
the k-space data. Furthermore, we exploit the partial sum minimization of
singular values to constrain the low-rankness of Hankel matrix. Results on
brain imaging data show that the proposed method outperforms the
state-of-the-art methods in terms of artifacts removal and our method
potentially has the ability to reconstruct high number of shot of DWI.
KEYWORDS: Diffusion weighted
imaging, Hankel matrix, image reconstruction, low-rankness, magnetic resonance
imaging.
Methods:
1.
Background
Diffusion weighted
magnetic resonance imaging (MRI) is a unique examining method noninvasively
detecting the Brownian motion of water molecules in the tissues in biomedical
imaging. It is widely used in tumor diagnosis, acute stroke evaluation and
neuroscience research. As a conventional method of diffusion weighted imaging
(DWI) acquisition, single-shot echo-planar imaging (EPI) has the advantages of
motion immunity and short acquisition time, but suffers from image distortion,
blurring and low spatial resolution. some methods were proposed to overcome the
distortion in DWI, such as spatiotemporal encoding and multi-shot EPI.
The multi-shot
interleaved EPI fully acquires the k-space data by sampling different segment
in each shot, as shown in Figure 1. Multi-shot EPI provides higher spatial
resolution than single-shot EPI. However, multi-shot is sensitive to
physiological motions, which will induce phase variations from shot to shot.
Directly interleaving multi-shot data together into fully sampled k-space will
lead to severe artifacts in image.

Figure
1. A
schematic diagram of 3-shot interleaved DWI. Note: The solid lines represent
the collecting lines in the k-space (Fourier space) of images, and the dotted
lines denote the lines where signals are not sampled.
2.
Phase-constrained
Low Rank Hankel Matrix reconstruction (PLRHM)
We exploit the partial sum of
singular values to constrain low-rankness, the proposed rank minimization model
is:
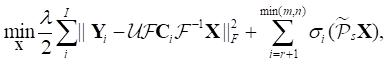
where ![]() denotes concatenated matrices of k-space
data of shots,
denotes concatenated matrices of k-space
data of shots, ![]() ,
,
![]() is an operator that converts
is an operator that converts ![]() into so called
into so called ![]() matrix in LORAKS
matrix in LORAKS ![]() the Fourier transform operator,
the Fourier transform operator, ![]() the inverse Fourier transform operator,
the inverse Fourier transform operator, ![]() the
the ![]() channel coil sensitivity map,
channel coil sensitivity map, ![]() an operator that under-samples k-space
data and zero-fills the non-sampled data points,
an operator that under-samples k-space
data and zero-fills the non-sampled data points, ![]() the
the ![]() channel sampled k-space data, where
channel sampled k-space data, where ![]() is the rank of
is the rank of ![]() ,
,
![]() the matrix size of
the matrix size of ![]() ,
,
![]() a regularization parameter that balances
the data consistency and low-rankness constraint.
a regularization parameter that balances
the data consistency and low-rankness constraint.
3.
Main
results
The proposed method was compared
with two state-of-the-art navigator-free DWI image reconstruction methods,
including the POCS-ICE and MUSSELS. Figure 2 show two slices reconstructions of
8-shot head DWI. Figure 2(d) exhibit the references reconstructed by IRIS.
Slight artifacts still remain in the reconstructions of POCS-ICE (Figure 2(a)),
as marked by red arrows. POCS-MUSSELS reconstructions (Figure 2(b)) show no
obvious artifacts but they look dark in the center of images, as marked by
yellow arrows. While our results (Figure 2(c)) can effectively reconstruct the
image with minimal artifacts.
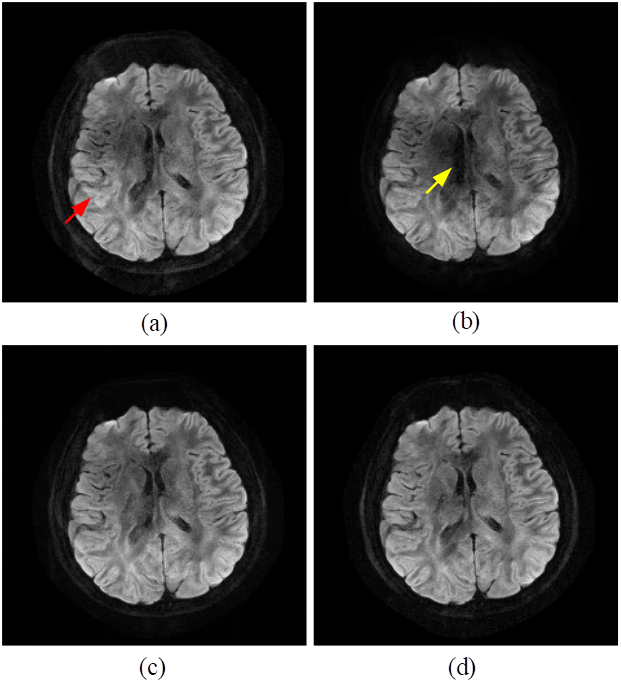
Figure
2. Reconstructions of slice 9 of 8-shot in
vivo head DWI using different reconstruction methods. (a) POCS-ICE, (b) POCS-MUSSELS,
(c) the proposed method, (d) reference reconstructed by IRIS. The residual
artifact is marked by the red arrow and the dark region is marked by yellow
arrow.
Figure 3 shows the reconstructions
of 3 slices of 12-shot head DWI. Directly inverse Fourier transformation induces
severe aliasing artifacts (Figure 3(a)). POCS-ICE fails to remove the severe
aliasing artifacts (Figure 3(b)). POCS-MUSSELS removes the artifacts to some
extent but slight artifacts still remain in the image (Figure 3(c)). While the
proposed method can effectively reconstruct the image with minimal artifacts
and shaper edges than POCS-MUSSELS, as shown in Figure 3(d). In this case, the
shot number is up to 12, which is an aggressive high shot number for
reconstruction. POCS-ICE and POCS-MUSSELS have difficulty to recover the
artifact-free image, while the proposed method has the potential to handle the case
with high number of shots.
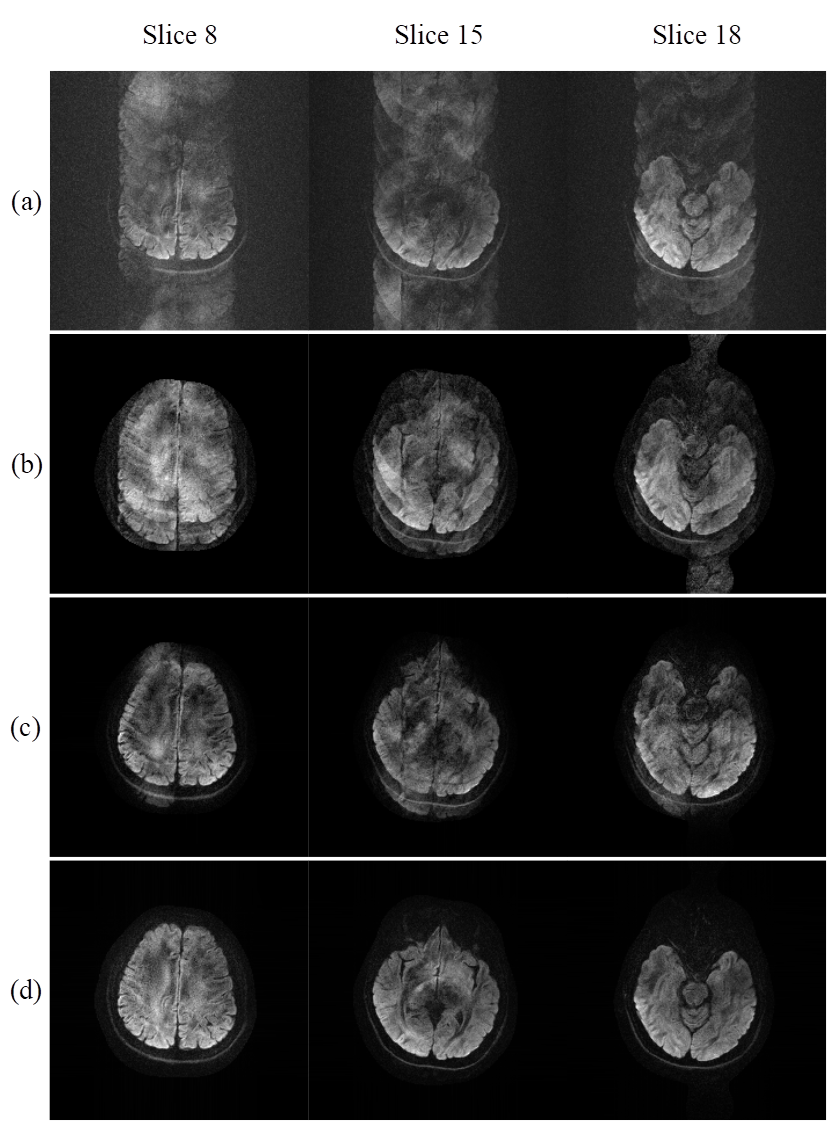
Figure
3. Reconstructions
of 3 slices of 12-shot in vivo head DWI
using different reconstruction methods. (a) direct reconstruction without
correction, (b) POCS-ICE, (c) POCS-MUSSELS, (d) the proposed method.
Acknowledgments:
This work was supported in
part by National Key R&D Program of China (2017YFC0108700), National
Natural Science Foundation of China (61971361, 61871341, 61811530021 and
61672335), Natural Science Foundation of Fujian Province of China (2018J06018),
Fundamental Research Funds for the Central Universities (20720180056), Science
and Technology Program of Xiamen (3502Z20183053), and China Scholarship
Council.
The authors would like to
thank Dr. Guobin Li in United Imaging Company for providing the 12-shot head
DWI data in this paper.
References:
[1] D.
Le Bihan, E. Breton, D. Lallemand, P. Grenier, E. Cabanis, and M.
Laval-Jeantet, "MR imaging of intravoxel incoherent motions: application
to diffusion and perfusion in neurologic disorders," Radiology, vol. 161, no. 2, pp. 401-407, 1986.
[2] D.
Le Bihan, J. F. Mangin, C. Poupon, C. A. Clark, S. Pappata, N. Molko, and H.
Chabriat, "Diffusion tensor imaging: concepts and applications," Journal of Magnetic Resonance Imaging, vol.
13, no. 4, pp. 534-546, 2001.
[3] S.
Mori and J. Zhang, "Principles of diffusion tensor imaging and its
applications to basic neuroscience research," Neuron, vol. 51, no. 5, pp. 527-539, 2006.
[4] A.
G. Sorensen, F. S. Buonanno, R. G. Gonzalez, L. H. Schwamm, M. H. Lev, F. R.
Huang-Hellinger, T. G. Reese, R. M. Weisskoff, T. L. Davis, and N. Suwanwela,
"Hyperacute stroke: evaluation with combined multisection
diffusion-weighted and hemodynamically weighted echo-planar MR imaging," Radiology, vol. 199, no. 2, pp. 391-401,
1996.
[5] M.
D. Budde and N. P. Skinner, "Diffusion MRI in acute nervous system
injury," Journal of Magnetic
Resonance, vol. 292, pp. 137-148, 2018.
[6] F.
Farzaneh, S. J. Riederer, and N. J. Pelc, "Analysis of T2 limitations and
off-resonance effects on spatial resolution and artifacts in echo-planar
imaging," Magnetic Resonance in
Medicine, vol. 14, no. 1, pp. 123-139, 1990.
[7] E.
Solomon, N. Shemesh, and L. Frydman, "Diffusion weighted MRI by
spatiotemporal encoding: analytical description and in vivo validations," Journal of Magnetic Resonance, vol. 232,
pp. 76-86, 2013.
[8] H.
K. Jeong, J. C. Gore, and A. W. Anderson, "High-resolution human diffusion
tensor imaging using 2-D navigated multishot SENSE EPI at 7 T," Magnetic Resonance in Medicine, vol. 69,
no. 3, pp. 793-802, 2013.
[9] X.
Ma, Z. Zhang, E. Dai, and H. Guo, "Improved multi-shot diffusion imaging
using GRAPPA with a compact kernel," Neuroimage,
vol. 138, pp. 88-99, 2016.
[10] N.
K. Chen, A. Guidon, H. C. Chang, and A. W. Song, "A robust multi-shot scan
strategy for high-resolution diffusion weighted MRI enabled by multiplexed
sensitivity-encoding (MUSE)," Neuroimage,
vol. 72, no. 2, pp. 41-47, 2013.
[11] H.
Guo, X. Ma, Z. Zhang, B. Zhang, C. Yuan, and F. Huang, "POCS‐enhanced
inherent correction of motion‐induced phase errors (POCS‐ICE) for
high‐resolution multishot diffusion MRI," Magnetic Resonance in Medicine, vol. 75, no. 1, pp. 169-180, 2016.
[12] M.
Mani, M. Jacob, D. Kelley, and V. Magnotta, "Multi‐shot
sensitivity‐encoded diffusion data recovery using structured low‐rank matrix
completion (MUSSELS)," Magnetic
Resonance in Medicine, vol. 78, no. 2, pp. 494-507, 2017.
[13] Y.
Hu, E. G. Levine, Q. Tian, C. J. Moran, X. Wang, V. Taviani, S. S. Vasanawala,
J. A. McNab, B. A. Daniel, and B. L. Hargreaves, "Motion‐robust
reconstruction of multishot diffusion‐weighted images without phase estimation
through locally low‐rank regularization," Magnetic Resonance in Medicine, vol. 81, no. 2, pp. 1181-1190,
2019.
[14] L.
Guo, F. Huang, Z. Xu, Y. Mei, W. Fang, X. Ma, E. Dai, H. Guo, Q. Feng, and W.
Chen, "eIRIS: Eigen-analysis approach for improved spine multi-shot
diffusion MRI," Magnetic Resonance
Imaging, vol. 50, pp. 134-140, 2018.
[15] W.
Liu, X. Zhao, Y. Ma, X. Tang, and J.-H. Gao, "DWI using navigated interleaved
multishot EPI with realigned GRAPPA reconstruction," Magnetic Resonance in Medicine, vol. 75, no. 1, pp. 280-286, 2016.
[16] E.
Dai, Z. Zhang, X. Ma, Z. Dong, X. Li, Y. Xiong, C. Yuan, and H. Guo, "The
effects of navigator distortion and noise level on interleaved EPI DWI
reconstruction: a comparison between image‐and k‐space‐based method," Magnetic Resonance in Medicine, vol. 80,
no. 5, pp. 2024-2032, 2018.
[17] K.
P. Pruessmann, M. Weiger, M. B. Scheidegger, and P. Boesiger, "SENSE:
sensitivity encoding for fast MRI," Magnetic
Resonance in Medicine, vol. 42, no. 5, pp. 952-962, 1999.
[18] X.
Zhang, D. Guo, Y. Huang, Y. Chen, L. Wang, F. Huang, and X. Qu, "Image
reconstruction with low-rankness and self-consistency of k-space data in
parallel MRI," arXiv preprint
arXiv:1909.02846, 2019.
[19] J.
P. Haldar, "Low-rank modeling of local k-space neighborhoods (LORAKS) for
constrained MRI," IEEE Transactions
on Medical Imaging, vol. 33, no. 3, pp. 668-681, 2013.
[20] K.
H. Jin, D. Lee, and J. C. Ye, "A general framework for compressed sensing
and parallel MRI using annihilating filter based low-rank Hankel matrix," IEEE Transactions on Computational Imaging, vol.
2, no. 4, pp. 480-495, 2016.
[21] G.
Ongie and M. Jacob, "Off-the-grid recovery of piecewise constant images
from few Fourier samples," SIAM
Journal on Imaging Sciences, vol. 9, no. 3, pp. 1004-1041, 2016.
[22] F.
Lam, C. Ma, B. Clifford, C. L. Johnson, and Z. P. Liang, "High‐resolution
1H‐MRSI of the brain using SPICE: data acquisition and image reconstruction,"
Magnetic Resonance in Medicine, vol.
76, no. 4, pp. 1059-1070, 2016.
[23] X.
Qu, M. Mayzel, J. F. Cai, Z. Chen, and V. Orekhov, "Accelerated NMR
spectroscopy with low‐rank reconstruction," Angewandte Chemie International Edition, vol. 54, no. 3, pp.
852-854, 2015.
[24] X.
Qu, Y. Huang, H. Lu, T. Qiu, D. Guo, T. Agback, V. Orekhov, and Z. Chen,
"Accelerated nuclear magnetic resonance spectroscopy with deep
learning," Angewandte Chemie
International Edition, DOI: 10.1002/anie.201908162, 2019.
[25] H.
Lu, X. Zhang, T. Qiu, J. Yang, J. Ying, D. Guo, Z. Chen, and X. Qu, "Low
rank enhanced matrix recovery of hybrid time and frequency data in fast
magnetic resonance spectroscopy," IEEE
Transactions on Biomedical Engineering, vol. 65, no. 4, pp. 809-820, 2017.
[26] J.
Ying, H. Lu, Q. Wei, J.-F. Cai, D. Guo, J. Wu, Z. Chen, and X. Qu, "Hankel
matrix nuclear norm regularized tensor completion for N-dimensional exponential
signals," IEEE Transactions on
Signal Processing, vol. 65, no. 14, pp. 3702-3717, 2017.
[27] J.
Ying, J.-F. Cai, D. Guo, G. Tang, Z. Chen, and X. Qu, "Vandermonde
factorization of Hankel matrix for complex exponential signal
recovery—Application in fast NMR spectroscopy," IEEE Transactions on Signal Processing, vol. 66, no. 21, pp. 5520-5533,
2018.
[28] G.
Ongie and M. Jacob, "Recovery of Piecewise Smooth Images from Few Fourier
Samples," In 2015 International
Conference on Sampling Theory and Applications (SampTA), pp. 543-547, 2015.
[29] P.
J. Shin, P. E. Z. Larson, M. A. Ohliger, M. Elad, J. M. Pauly, D. B. Vigneron,
and M. Lustig, "Calibrationless parallel imaging reconstruction based on
structured low-rank matrix completion," Magnetic Resonance in Medicine, vol. 72, no. 4, pp. 959-970, 2014.
[30] J.
P. Haldar and J. Zhuo, "P-LORAKS: Low-rank modeling of local k-space
neighborhoods with parallel imaging data," Magnetic Resonance in Medicine, vol. 75, no. 4, pp. 1499-1514.
[31] T.
H. Kim, K. Setsompop, and J. P. Haldar, "LORAKS makes better SENSE:
Phase-constrained partial fourier SENSE reconstruction without phase
calibration," Magnetic Resonance in
Medicine, vol. 77, no. 3, pp. 1021-1035, 2017.
[32] Z.-P.
Liang, "Spatiotemporal imaging with partially separable functions,"
in 2007 4th IEEE International Symposium
on Biomedical Imaging: From Nano to Macro, 2007, pp. 988-991: IEEE.
[33] B.
Zhao, J. P. Haldar, A. G. Christodoulou, and Z.-P. Liang, "Image
reconstruction from highly undersampled (k, t)-space data with joint partial
separability and sparsity constraints," IEEE Transactions on Medical Imaging, vol. 31, no. 9, pp.
1809-1820, 2012.
[34] S.
G. Lingala, Y. Hu, E. DiBella, and M. Jacob, "Accelerated dynamic MRI
exploiting sparsity and low-rank structure: kt SLR," IEEE Transactions on Medical Imaging, vol. 30, no. 5, pp.
1042-1054, 2011.
[35] R.
A. Lobos, T. H. Kim, W. S. Hoge, and J. P. Haldar, "Navigator-free EPI
ghost correction with structured low-rank matrix models: New theory and
methods," IEEE Transactions on
Medical Imaging, vol. 37, no. 11, pp. 2390-2402, 2018.
[36] Z.
Hu, X. Ma, T.-K. Truong, A. W. Song, and H. Guo, "Phase-updated
regularized SENSE for navigator-free multishot diffusion imaging," Magnetic Resonance in Medicine, vol. 78,
no. 1, pp. 172-181, 2017.
[37] B.
Recht, M. Fazel, and P. A. Parrilo, "Guaranteed minimum-rank solutions of
linear matrix equations via nuclear norm minimization," SIAM Review, vol. 52, no. 3, pp.
471-501, 2010.
[38] Y.
Hu, D. Zhang, J. Ye, X. Li, and X. He, "Fast and accurate matrix
completion via truncated nuclear norm regularization," IEEE Transactions on Pattern Analysis and
Machine Intelligence, vol. 35, no. 9, pp. 2117-2130, 2012.
[39] T.-H.
Oh, H. Kim, Y.-W. Tai, J.-C. Bazin, and I. So Kweon, "Partial sum
minimization of singular values in RPCA for low-level vision," in Proceedings of the IEEE International
Conference on Computer Vision, 2013, pp. 145-152.
[40] S.
Boyd, N. Parikh, E. Chu, B. Peleato, and J. Eckstein, "Distributed
optimization and statistical learning via the alternating direction method of
multipliers," Foundations and
Trends® in Machine learning, vol. 3, no. 1, pp. 1-122, 2011.
[41] R.
Chandra, S. Eisenstat, and M. Schultz, "Conjugate gradient methods for
partial differential equations," Yale University New Haven, CT, 1978.
[42] T.-H.
Oh, Y. Matsushita, Y.-W. Tai, and I. So Kweon, "Fast randomized singular
value thresholding for nuclear norm minimization," in Proceedings of the IEEE Conference on Computer Vision and Pattern
Recognition, 2015, pp. 4484-4493.
[43] G.
H. Golub and C. F. Van Loan, "Matrix computations," The Johns Hopkins University Press,
Baltimore, USA, 1989.
[44] M.
Uecker, P. Lai, M. J. Murphy, P. Virtue, M. Elad, J. M. Pauly, S. S.
Vasanawala, and M. Lustig, "ESPIRiT—an eigenvalue approach to
autocalibrating parallel MRI: Where SENSE meets GRAPPA," Magnetic Resonance in Medicine, vol. 71,
no. 3, pp. 990-1001, 2014.
[45] B. Bilgic, I. Chatnuntawech, M. K. Manhard, Q. Tian, C. Liao, S. S. Iyer, S. F. Cauley, S. Y. Huang, J. R. Polimeni, and L. L. Wald, "Highly accelerated multishot echo planar imaging through synergistic machine learning and joint reconstruction," Magnetic Resonance in Medicine, vol. 82, pp. 1343-1358, 2019.