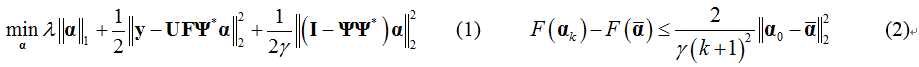Projected Fast Iterative Soft-Thresholding Algorithm (pFISTA) for Tight Frames in Sparse MRI Image Reconstruction
-Balanced Sparse MRI with Fast Reconstruction and Minimal Parameters
Yunsong Liu1, Zhifang Zhan1, Jian-Feng Cai2, Di Guo3, Zhong Chen1, Xiaobo Qu1,*
1 Department of Electronic Science, Fujian Provincial Key Laboratory of Plasma and Magnetic Resonance, Xiamen University, Xiamen, China
2 Department of Mathematics, Hong Kong University of Science and Technology, Hong Kong, China
3 School of Computer and Information Engineering, Xiamen University of Technology, Xiamen, China
* Email: yunsongliu<at>stu.xmu.edu.cn or quxiaobo <at> xmu.edu.cn or quxiaobo2009 <at> gmail.com .
Compressed sensing (CS) has exhibited great potential for accelerating magnetic resonance imaging (MRI). In CS-MRI, we want to reconstruct a high-quality image from very few samples in a short time. It has been shown that, redundant image representations, e.g. frames, can significantly improve the image quality. But how to efficiently solve the reconstruction problem with these redundant representation systems is still challenging.
This work address the problem of applying fast iterative soft-thresholding algorithm (FISTA) [1-3] to analysis sparse model based CS-MRI [4-7] reconstruction problems under tight frame representation systems. We first rewrite the analysis model to be a constrained synthesis-like one. Then we propose to approximate a constrained proximal map by an unconstrained proximal map plus the orthogonal projection onto the constrained subspace. This results in our proposed projected iterative soft-thresholding algorithm (pISTA). By incorporating the accelerating strategy for FISTA, we obtain the accelerated version pFISTA. We prove that pFISTA converges to a balance sparse model [8-10]. Numerical results show that pFISTA achieves better reconstruction than FISTA for synthesis sparse models [3] and converges faster than or comparable to the state-of-the-art SFISTA [11].
The pFISTA introduces only one adjustable parameter, the step size, and we provide an explicit rule to set this parameter. Numerical results demonstrate tha reconstruction errors incurred by pFISTA appear insensitive to the step size. It is expected that this fast and efficient iterative thresolding algorithm will be useful for magnetic resonance image reconstruction in fast MRI applications.
The demo code of pFISTA can be downloaded here.
Please cite this paper when using the pFISTA code or any software derived from it.
The citation is: Yunsong Liu, Zhifang Zhan, Jian-Feng Cai, Di Guo, Zhong Chen, Xiaobo Qu. Projected iterative soft-thresholding algorithm for tight frames in compressed sensing magnetic resonance imaging, IEEE Transactions on Medical Imaging, DOI:10.1109/TMI.2016.2550080, 2016.
1. Yunsong Liu, Zhifang Zhan, Jian-Feng Cai, Di Guo, Zhong Chen, Xiaobo Qu. Projected iterative soft-thresholding algorithm for tight frames in compressed sensing magnetic resonance imaging, IEEE Transactions on Medical Imaging, DOI:10.1109/TMI.2016.2550080, 2016. 
.png) [Code]
[Code]
2. Yunsong Liu, Zhifang Zhan, Jian-Feng Cai, Di Guo, Zhong Chen, Xiaobo Qu. Projected Iterative Soft-thresholding Algorithm for Tight Frames in Compressed Sensing Magnetic Resonance Imaging, arXiv:1504.07786, 2015. (Submitted on 29 Apr 2015 (v1), last revised 3 Oct 2015 (v2)) [Code]
3. Yunsong Liu, Zhifang Zhan, Jian-Feng Cai, Di Guo, Zhong Chen, Xiaobo Qu. Projected fast iterative soft threshold algorithm for frames-based compressed sensing MRI, International Society of Magnetic Resonance-ISMAR’15, 16th – 21st, August, 2015. (Oral presentation, Student Travel Stipend)
4. Yunsong Liu, Jian-Feng Cai, Zhifang Zhan,Di Guo,Jing Ye,Zhong Chen, Xiaobo Qu. Balanced sparse model for tight frames in compressed sensing magnetic resonance imaging, PLoS ONE, 10(4): e0119584, 2015. .png) [Code] [Dataset]
[Code] [Dataset]
5. Yunsong Liu, Jian-Feng Cai, Zhifang Zhan, Di Guo, Jing Ye, Zhong Chen, Xiaobo Qu. Balanced sparse MRI model: Bridge the analysis and synthesis sparse models in compressed sensing MRI, pp. 3423, International Society for Magnetic Resonance in Medicine 23rd Scientific Meeting-ISMRM'15. Milanno-ISMRM’15, Toronto, Canada, May 30-June 5, 2015. .png) [Code]
[Code]
6. Yunsong Liu, Zhifang Zhan, Jian-Feng Cai, Jing Ye, Zhong Chen, Xiaobo Qu. Balance sparsity model for tight-frame representation in compressed sensing MRI, 2014 IEEE International Symposium on Biomedical Imaging-ISBI’14, FrA06.16, Beijing, China, April 29- May 2, 2014. .png) [Code]
[Code]

Theorem: Let 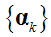 and
and 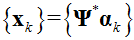 be sequences generated by pFISTA implemented in coefficient domain and image domain respectively. Provided that the step size
be sequences generated by pFISTA implemented in coefficient domain and image domain respectively. Provided that the step size 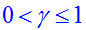 and
and 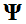 is a tight frame, then
is a tight frame, then 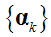 converges to a solution of (1) with the speed (2) where
converges to a solution of (1) with the speed (2) where 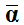 is a solution of (1) and F is the objective function in (1).
is a solution of (1) and F is the objective function in (1).
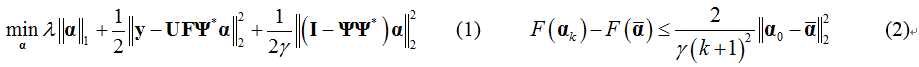
1. gama=1 is optimal for fastest convergence and easy implementation.
2. Reconstructions of T2-weighted brain image using FISTA for synthesis models [3], SFISTA [11]and pFISTA for analysis models.

3. Comparisons of empirical convergence speed.

Note: All numerical experiments are conducted on a Dell PC running Windows 7 operating system with Intel Core i7 2600 CPU. For quantitative comparison, we adopt the relative L2 norm error (RLNE) defined as
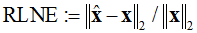 ,
,
where 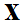 is the ground truth image and
is the ground truth image and 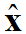 is the reconstructed image.
is the reconstructed image.
This work was supported by the National Natural Science Foundation of China (61571380, 61201045, 61302174 and 11375147), Natural Science Foundation of Fujian Province of China (2015J01346 and 2016J05205), Important Joint Research Project on Major Diseases of Xiamen City (3502Z20149032), Fundamental Research Funds for the Central Universities (20720150109, 2013SH002) and NSF DMS-1418737.
[1] Y. Nesterov, "A method of solving a convex programming problem with convergence rate O (1/k2)," Soviet Mathematics Doklady, vol. 27, pp. 372-376, 1983.
[2] P. Combettes and V. Wajs, "Signal recovery by proximal forward-backward splitting," Multiscale Modeling & Simulation, vol. 4, pp. 1168-1200, 2005.
[3] A. Beck and M. Teboulle, "A fast iterative shrinkage-thresholding algorithm for linear inverse problems," SIAM Journal on Imaging Sciences, vol. 2, pp. 183-202, 2009.
[4] M. Lustig, D. Donoho, and J. M. Pauly, "Sparse MRI: The application of compressed sensing for rapid MR imaging," Magnetic Resonance in Medicine, vol. 58, pp. 1182-1195, Dec 2007.
[5] X. Qu, Y. Hou, F. Lam, D. Guo, J. Zhong, and Z. Chen, "Magnetic resonance image reconstruction from undersampled measurements using a patch-based nonlocal operator," Medical Image Analysis, vol. 18, pp. 843-856, 2014.
[6] X. Qu, D. Guo, B. Ning, Y. Hou, Y. Lin, S. Cai, and Z. Chen, "Undersampled MRI reconstruction with patch-based directional wavelets," Magnetic Resonance Imaging, vol. 30, pp. 964-977, 2012.
[7] E. J. Candes, Y. C. Eldar, D. Needell, and P. Randall, "Compressed sensing with coherent and redundant dictionaries," Applied and Computational Harmonic Analysis, vol. 31, pp. 59-73, 2011.
[8] Y. Liu, J.-F. Cai, Z. Zhan, D. Guo, J. Ye, Z. Chen, and X. Qu., "Balanced sparse model for tight frames in compressed sensing magnetic resonance imaging," Plos One, vol. 10, p. e0119584, 2015.
[9] J.-F. Cai, S. Osher, and Z. Shen, "Split Bregman methods and frame based image restoration," Multiscale Modeling & Simulation, vol. 8, pp. 337-369, 2009.
[10] Z. Shen, K.-C. Toh, and S. Yun, "An accelerated proximal gradient algorithm for frame-based image restoration via the balanced approach," SIAM Journal on Imaging Sciences, vol. 4, pp. 573-596, 2011.
[11] Z. Tan, Y. C. Eldar, A. Beck, and A. Nehorai, "Smoothing and decomposition for analysis sparse recovery," IEEE Transactions on Signal Processing, vol. 62, pp. 1762-1774, 2014.